5 Ways To Interpolate

Introduction to Interpolation

Interpolation is a fundamental concept in various fields, including mathematics, computer science, and engineering. It involves estimating or finding the value of a function or a data point within a given interval or range. Interpolation techniques are widely used in data analysis, signal processing, and machine learning. In this article, we will discuss five ways to interpolate, highlighting their strengths, weaknesses, and applications.

1. Linear Interpolation

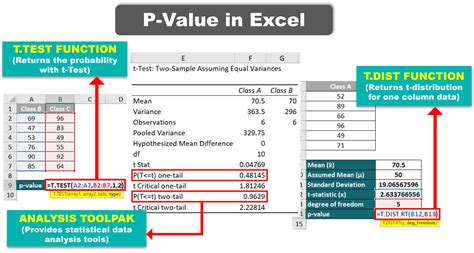
Linear interpolation is the simplest and most common interpolation technique. It involves connecting two known data points with a straight line and estimating the value of the function at a point within this interval. Linear interpolation is based on the assumption that the function is linear between the two known points. The formula for linear interpolation is: y = y1 + (x - x1) * (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are the known data points, and (x, y) is the point to be interpolated.

2. Polynomial Interpolation

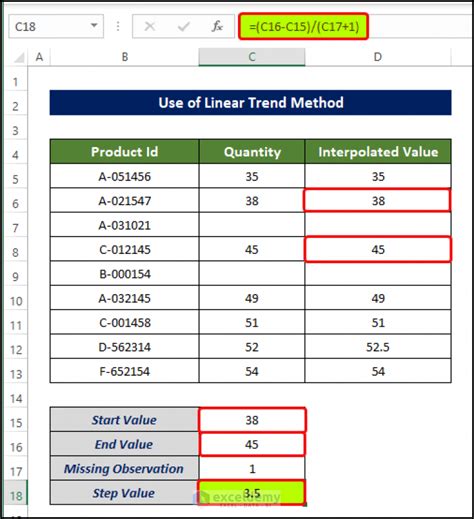
Polynomial interpolation involves fitting a polynomial curve to a set of known data points. The degree of the polynomial is typically one less than the number of data points. Polynomial interpolation can be used to model complex relationships between variables. However, it can also lead to overfitting, especially when dealing with noisy data. The formula for polynomial interpolation is: y = a0 + a1 * x + a2 * x^2 +… + an * x^n where a0, a1,…, an are the coefficients of the polynomial, and n is the degree of the polynomial.

3. Spline Interpolation

Spline interpolation involves fitting a piecewise continuous curve to a set of known data points. The curve is composed of multiple segments, each representing a different interval. Spline interpolation is useful for modeling complex relationships between variables, especially when dealing with large datasets. There are several types of splines, including linear, quadratic, and cubic splines. The formula for spline interpolation is: y = f(x) = ∑[ai * bi(x)] where ai are the coefficients, and bi(x) are the basis functions.

4. Nearest Neighbor Interpolation

Nearest neighbor interpolation involves estimating the value of a function at a point based on the value of the nearest known data point. Nearest neighbor interpolation is simple to implement and can be useful when dealing with large datasets. However, it can also lead to poor estimates, especially when the data points are sparse. The formula for nearest neighbor interpolation is: y = yj where yj is the value of the nearest known data point.

5. Cubic Interpolation

Cubic interpolation involves fitting a cubic curve to a set of known data points. Cubic interpolation is useful for modeling complex relationships between variables, especially when dealing with smooth curves. The formula for cubic interpolation is: y = a0 + a1 * x + a2 * x^2 + a3 * x^3 where a0, a1, a2, and a3 are the coefficients of the cubic curve.

Interpolation Method	Description	Strengths	Weaknesses
Linear Interpolation	Connecting two known data points with a straight line	Simple to implement, fast computation	Assumes linearity, can lead to poor estimates
Polynomial Interpolation	Fitting a polynomial curve to a set of known data points	Can model complex relationships, flexible	Can lead to overfitting, computationally expensive
Spline Interpolation	Fitting a piecewise continuous curve to a set of known data points	Can model complex relationships, smooth curves	Computationally expensive, can be difficult to implement
Nearest Neighbor Interpolation	Estimating the value of a function at a point based on the value of the nearest known data point	Simple to implement, fast computation	Can lead to poor estimates, especially with sparse data
Cubic Interpolation	Fitting a cubic curve to a set of known data points	Can model complex relationships, smooth curves	Computationally expensive, can be difficult to implement

💡 Note: The choice of interpolation method depends on the specific problem, the nature of the data, and the desired level of accuracy.

In summary, interpolation is a powerful tool for estimating or finding the value of a function or a data point within a given interval or range. The five interpolation methods discussed in this article, including linear, polynomial, spline, nearest neighbor, and cubic interpolation, each have their strengths and weaknesses. By understanding the characteristics of each method, practitioners can choose the most suitable technique for their specific application.