5 Ways Anova Test

Introduction to Anova Test

The Anova test, or Analysis of Variance, is a statistical technique used to compare means of three or more samples to find out if at least one of the means is different. This test is widely used in various fields, including business, medicine, and social sciences. In this article, we will explore 5 ways the Anova test can be applied in different scenarios.

What is Anova Test?

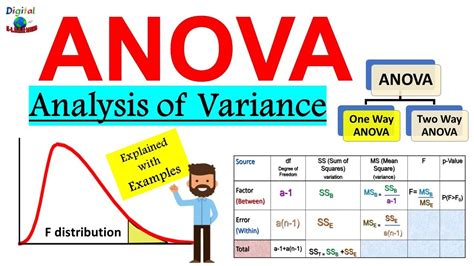
The Anova test is a powerful tool that helps to determine if there are any significant differences between the means of two or more groups. It is commonly used to analyze data from experiments, surveys, and observational studies. The test works by comparing the variance between the groups to the variance within the groups. If the variance between the groups is significantly greater than the variance within the groups, it indicates that at least one of the means is different.

5 Ways Anova Test Can Be Applied

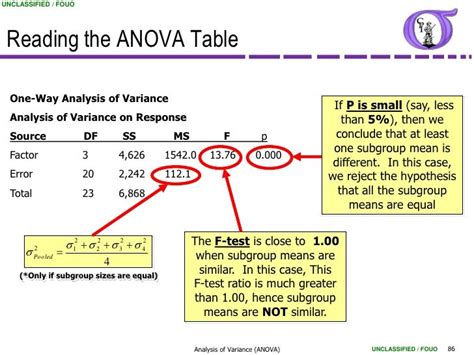
Here are 5 ways the Anova test can be applied in different scenarios: * Comparing Means of Multiple Groups: The Anova test can be used to compare the means of three or more groups to find out if at least one of the means is different. For example, a researcher may want to compare the average scores of students from different schools to see if there are any significant differences. * Analyzing Experimental Data: The Anova test can be used to analyze data from experiments to determine if there are any significant differences between the treatment groups. For example, a researcher may want to compare the average response times of participants who received different treatments. * Identifying Significant Differences: The Anova test can be used to identify significant differences between the means of two or more groups. For example, a marketer may want to compare the average sales of different products to see if there are any significant differences. * Determining the Effect of a Variable: The Anova test can be used to determine the effect of a variable on a response variable. For example, a researcher may want to study the effect of temperature on the growth rate of plants. * Validating Assumptions: The Anova test can be used to validate assumptions about the data, such as the assumption of equal variances. For example, a researcher may want to check if the variances of the different groups are equal before proceeding with further analysis.

Example of Anova Test

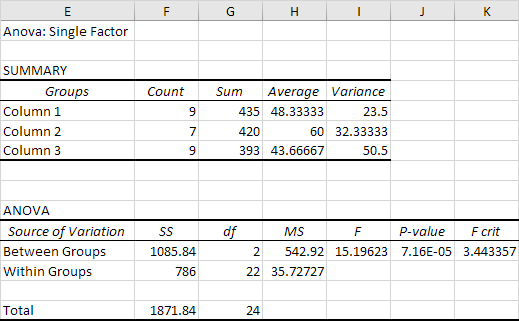
Suppose we want to compare the average scores of students from three different schools. We collect a sample of 10 students from each school and calculate the average scores. The results are as follows:

School	Average Score
School A	85
School B	90
School C	78

We can use the Anova test to determine if there are any significant differences between the average scores of the three schools. The test statistic is calculated as follows: F = (MSB / MSE) where MSB is the mean square between the groups and MSE is the mean square error. The p-value is then calculated using the F-distribution. If the p-value is less than the significance level (usually 0.05), we reject the null hypothesis and conclude that at least one of the means is different.

📝 Note: The Anova test assumes that the data is normally distributed and that the variances of the different groups are equal. If these assumptions are not met, alternative tests such as the Kruskal-Wallis test may be used.

Conclusion and Future Directions

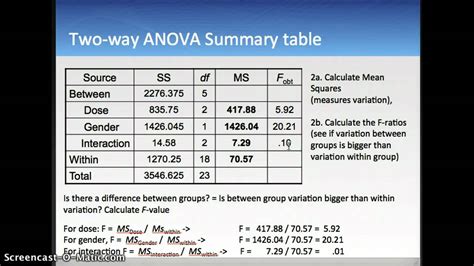
In conclusion, the Anova test is a powerful tool that can be used to compare means of three or more groups. It has a wide range of applications in various fields, including business, medicine, and social sciences. By understanding how to apply the Anova test, researchers and analysts can make informed decisions and draw meaningful conclusions from their data. Future directions for the Anova test include developing new methods for handling non-normal data and unequal variances, as well as exploring new applications in emerging fields such as data science and machine learning.