5 Ways To Calculate Z-Score
Introduction to Z-Score Calculation
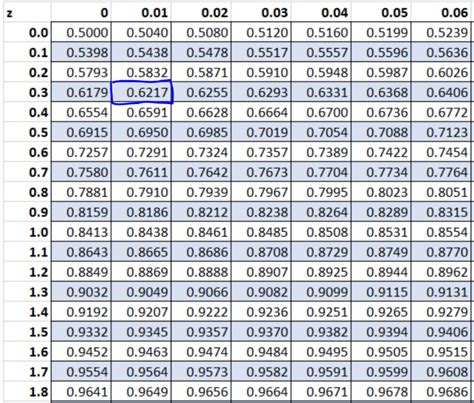
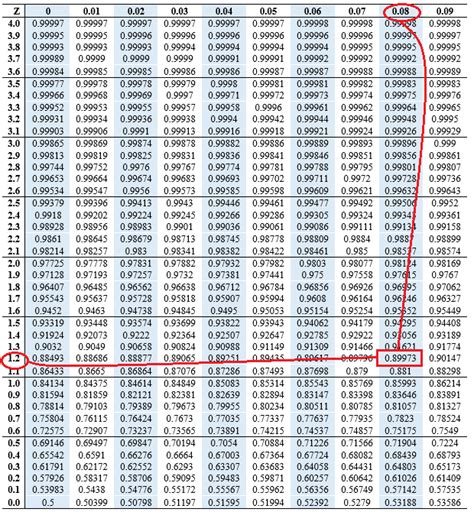
The z-score, also known as the standard score, is a statistical measure that describes a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean. If a value has a z-score of 0, it is equal to the mean. A z-score greater than 0 means the value is above the mean, while a z-score less than 0 means the value is below the mean. In this article, we will explore 5 ways to calculate z-scores and understand their applications.
Understanding Z-Score Formula

The basic formula to calculate a z-score is: [ z = \frac{(X - \mu)}{\sigma} ] where: - ( z ) is the z-score, - ( X ) is the value of the element, - ( \mu ) is the mean of the dataset, - ( \sigma ) is the standard deviation of the dataset.
Method 1: Manual Calculation
To manually calculate the z-score, follow these steps: - Find the mean (( \mu )) of your dataset. - Calculate the standard deviation (( \sigma )) of your dataset. - Subtract the mean from your target value (( X - \mu )). - Divide the result by the standard deviation.
For example, if your dataset is {1, 2, 3, 4, 5}, the mean (( \mu )) is 3, and the standard deviation (( \sigma )) is approximately 1.414. To find the z-score of the value 4: [ z = \frac{(4 - 3)}{1.414} \approx \frac{1}{1.414} \approx 0.707 ]
Method 2: Using a Z-Score Calculator

There are many online z-score calculators available that can simplify the process. You just need to input the value, the mean, and the standard deviation, and the calculator will give you the z-score. This method is quicker and reduces the chance of human error.
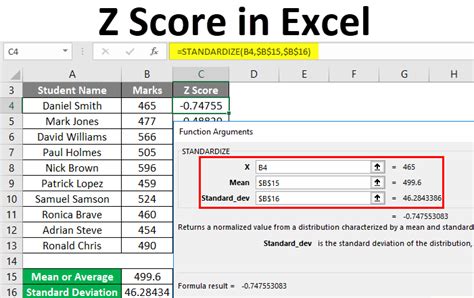
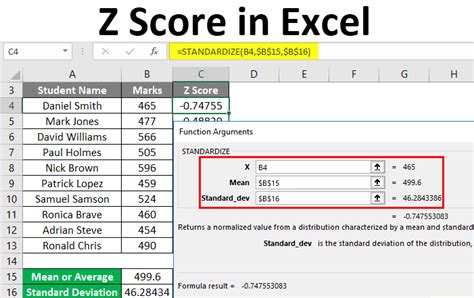
Method 3: Microsoft Excel

In Microsoft Excel, you can calculate the z-score using the following formula: [ z = \frac{(X - \text{AVERAGE(dataset)})}{\text{STDEV(dataset)}} ] Assuming your dataset is in cells A1 through A5, and you want to find the z-score of the value in cell A6, the formula would be: [ z = \frac{(A6 - \text{AVERAGE(A1:A5)})}{\text{STDEV(A1:A5)}} ]
Method 4: Programming Languages

Many programming languages, such as Python, R, and MATLAB, have built-in functions or libraries to calculate z-scores. For example, in Python using the scipy library, you can calculate the z-score as follows:
from scipy import stats
# Sample dataset
data = [1, 2, 3, 4, 5]
value = 4
# Calculate mean and standard deviation
mean = sum(data) / len(data)
std_dev = stats.tstd(data)
# Calculate z-score
z_score = (value - mean) / std_dev
print(z_score)
Method 5: Statistical Software

Statistical software packages like R, SPSS, and SAS also provide functions to calculate z-scores. These tools are particularly useful for large datasets and complex statistical analyses.
📝 Note: Always ensure your data is normally distributed or nearly normally distributed for z-scores to be meaningful, as the z-score calculation assumes a normal distribution.
In summary, calculating z-scores can be done in various ways, ranging from manual calculations to using specialized software. Each method has its own advantages, and the choice of method depends on the specific requirements of the analysis, the size and complexity of the dataset, and personal preference.
| Method | Description | Advantages |
|---|---|---|
| Manual Calculation | Using the formula z = (X - μ) / σ | Understanding of the formula, applicable for small datasets |
| Z-Score Calculator | Online tools for quick calculation | Fast, reduces human error |
| Microsoft Excel | Using Excel formulas | Convenient for those familiar with Excel, applicable for medium-sized datasets |
| Programming Languages | Using libraries or functions in programming languages | Flexible, powerful for large datasets and automation |
| Statistical Software | Using specialized statistical software | Robust, suitable for complex analyses and large datasets |
Ultimately, the z-score is a powerful tool for understanding the position of a value within a dataset. By choosing the most appropriate method for calculating z-scores based on the context and requirements of the analysis, researchers and analysts can gain valuable insights into their data.
What is the purpose of calculating z-scores?

+
The purpose of calculating z-scores is to understand how many standard deviations an element is from the mean. This helps in comparing data points from different datasets and in identifying outliers or unusual values.
Can z-scores be used for non-normally distributed data?

+
While z-scores assume a normal distribution, they can still be used for non-normally distributed data for a general comparison. However, for precise statistical inferences, transformations or alternative methods might be necessary to ensure the data meets the assumptions of normality.
How do I choose the best method for calculating z-scores?

+
The choice of method depends on the size and complexity of the dataset, personal familiarity with software or programming languages, and the need for precision versus speed. For small datasets and educational purposes, manual calculation or online calculators might suffice. For larger datasets or professional analyses, software or programming languages are often more efficient.