5 Ways Calculate Sharpe Ratio

Introduction to Sharpe Ratio

The Sharpe ratio is a financial metric that helps investors understand the relationship between risk and return of an investment. It is the average return earned in excess of the risk-free rate per unit of volatility or total risk. The Sharpe ratio is named after William F. Sharpe, who developed it in the 1960s. The ratio is calculated as the difference between the average return of an investment and the average return of a risk-free asset, divided by the standard deviation of the investment’s returns. In this article, we will discuss five ways to calculate the Sharpe ratio and its importance in investment decisions.

Understanding the Formula

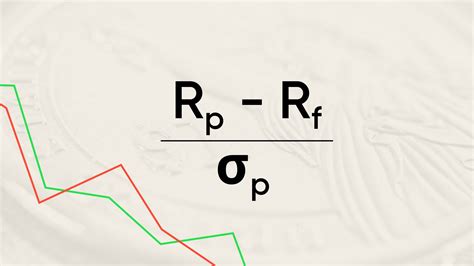
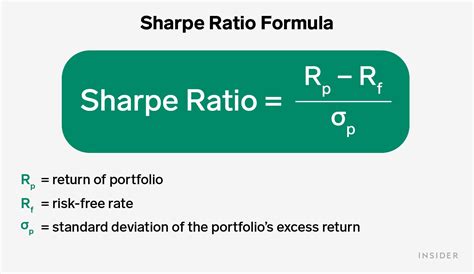
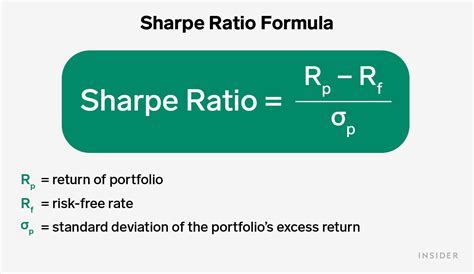
Before diving into the different methods of calculating the Sharpe ratio, it’s essential to understand the basic formula. The Sharpe ratio formula is as follows: Sharpe Ratio = (Rp - Rf) / σp Where: - Rp = Average return of the investment - Rf = Average return of a risk-free asset - σp = Standard deviation of the investment’s returns The higher the Sharpe ratio, the better the investment’s risk-adjusted return.

Method 1: Using Historical Data

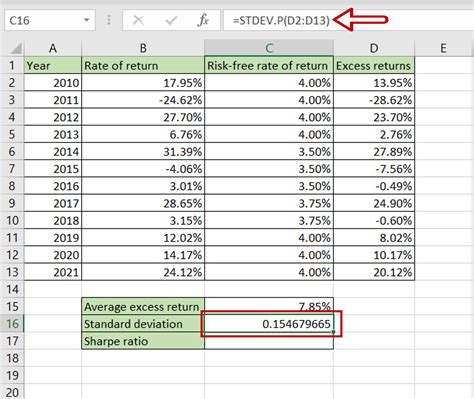
One way to calculate the Sharpe ratio is by using historical data. This method involves calculating the average return and standard deviation of the investment’s returns over a specific period. The risk-free rate is typically represented by the return on a short-term government bond, such as a U.S. Treasury bill. To calculate the Sharpe ratio using historical data, follow these steps: * Collect historical return data for the investment and the risk-free asset * Calculate the average return for both the investment and the risk-free asset * Calculate the standard deviation of the investment’s returns * Plug the values into the Sharpe ratio formula

Method 2: Using Expected Returns

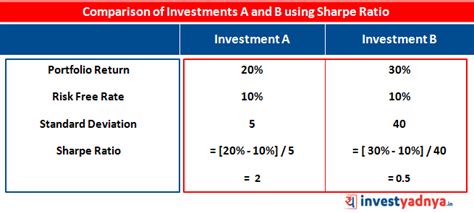
Another way to calculate the Sharpe ratio is by using expected returns. This method is useful when historical data is not available or when investors want to forecast future performance. To calculate the Sharpe ratio using expected returns, follow these steps: * Estimate the expected return of the investment * Estimate the expected return of the risk-free asset * Estimate the expected standard deviation of the investment’s returns * Plug the values into the Sharpe ratio formula It’s essential to note that expected returns are based on forecasts and may not reflect actual performance.

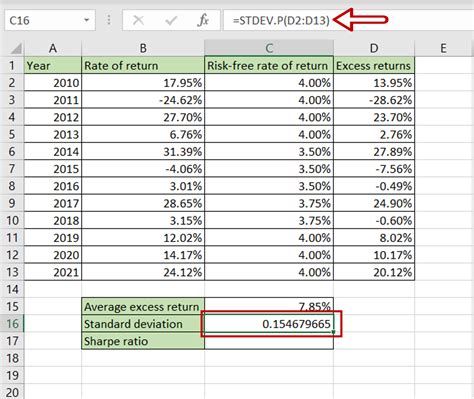
Method 3: Using a Spreadsheet

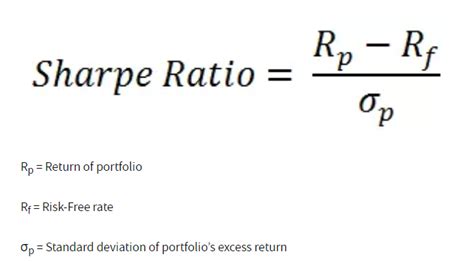
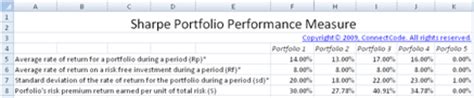
Calculating the Sharpe ratio can be simplified using a spreadsheet. Most spreadsheet software, such as Microsoft Excel, has built-in functions for calculating averages and standard deviations. To calculate the Sharpe ratio using a spreadsheet, follow these steps: * Enter the historical return data for the investment and the risk-free asset into the spreadsheet * Use the average function to calculate the average return for both the investment and the risk-free asset * Use the standard deviation function to calculate the standard deviation of the investment’s returns * Create a formula to calculate the Sharpe ratio using the values calculated above Using a spreadsheet can save time and reduce errors when calculating the Sharpe ratio.

Method 4: Using a Financial Calculator

A financial calculator can also be used to calculate the Sharpe ratio. Most financial calculators have built-in functions for calculating averages, standard deviations, and ratios. To calculate the Sharpe ratio using a financial calculator, follow these steps: * Enter the historical return data for the investment and the risk-free asset into the calculator * Use the calculator’s functions to calculate the average return and standard deviation of the investment’s returns * Use the calculator’s ratio function to calculate the Sharpe ratio Financial calculators can be a convenient way to calculate the Sharpe ratio, especially for investors who need to make quick decisions.

Method 5: Using a Programming Language

Finally, the Sharpe ratio can be calculated using a programming language, such as Python or R. This method is useful for investors who need to calculate the Sharpe ratio for large portfolios or who want to automate the calculation process. To calculate the Sharpe ratio using a programming language, follow these steps: * Import the necessary libraries and load the historical return data for the investment and the risk-free asset * Use the programming language’s functions to calculate the average return and standard deviation of the investment’s returns * Create a function to calculate the Sharpe ratio using the values calculated above Using a programming language can be a powerful way to calculate the Sharpe ratio, especially for complex portfolios.

📝 Note: The Sharpe ratio is just one metric used to evaluate investment performance. It's essential to consider other metrics, such as the Treynor ratio and the Sortino ratio, to get a comprehensive view of an investment's risk-adjusted return.

In summary, the Sharpe ratio is a valuable metric for evaluating investment performance. There are five ways to calculate the Sharpe ratio: using historical data, expected returns, a spreadsheet, a financial calculator, and a programming language. Each method has its advantages and disadvantages, and investors should choose the method that best suits their needs. By understanding the Sharpe ratio and how to calculate it, investors can make more informed decisions about their investments.