5 Ways To Calculate Mad

Introduction to Calculating Mean Absolute Deviation (MAD)

Calculating the Mean Absolute Deviation (MAD) is a statistical method used to measure the average distance between each data point and the mean of the dataset. It provides a way to understand the spread or dispersion of data from its central tendency. In this article, we’ll explore five ways to calculate MAD, highlighting the steps, importance, and applications of this statistical measure in various fields.

Understanding Mean Absolute Deviation (MAD)

Before diving into the methods, it’s essential to grasp what MAD signifies. The Mean Absolute Deviation is a measure that calculates the average of the absolute differences between each data point and the mean. It is a more interpretable measure than the standard deviation for many because it is in the same units as the data. MAD is particularly useful in data analysis for identifying how spread out the values in a dataset are from the average value.

Method 1: Manual Calculation

The most straightforward way to calculate MAD is by manually computing the absolute differences of each data point from the mean, summing these differences, and then dividing by the number of observations. The steps involve: - Calculating the mean of the dataset. - Finding the absolute difference between each data point and the mean. - Summing up these absolute differences. - Dividing the sum by the number of data points.

For example, if we have the dataset {1, 2, 3, 4, 5}, the mean is 3. The absolute differences from the mean are |1-3|, |2-3|, |3-3|, |4-3|, |5-3|, which are 2, 1, 0, 1, 2 respectively. The sum of these differences is 2+1+0+1+2 = 6. Dividing by the number of observations (5), we get MAD = ⁶⁄₅ = 1.2.

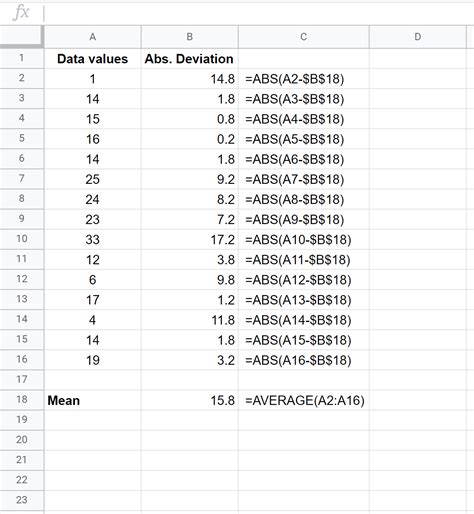
Method 2: Using Excel

For larger datasets, using a spreadsheet program like Excel can significantly simplify the calculation of MAD. The steps involve: - Entering the dataset into a column. - Calculating the mean using the AVERAGE function. - Calculating the absolute difference of each data point from the mean using the ABS function. - Summing these differences and dividing by the number of observations.

Excel formulas can automate this process. For instance, if data is in column A from A1 to A5, the mean can be calculated as =AVERAGE(A1:A5), and the absolute deviations can be summed and averaged using =AVERAGE(ABS(A1:A5-$mean)), where $mean is the cell containing the mean value.

Method 3: Using Python

Python, with its extensive libraries such as NumPy and Pandas, offers a powerful way to calculate MAD. The numpy library provides functions for calculating the mean, and then you can use list comprehension or vectorized operations to calculate the absolute deviations.

import numpy as np

# Sample dataset
data = np.array([1, 2, 3, 4, 5])

# Calculate mean
mean = np.mean(data)

# Calculate absolute deviations
abs_dev = np.abs(data - mean)

# Calculate MAD
mad = np.mean(abs_dev)

print(mad)

Method 4: Using R

R is another statistical computing environment that can be used to calculate MAD efficiently. The mean function calculates the mean, and then you can use vectorized operations to find the absolute deviations.

# Sample dataset
data <- c(1, 2, 3, 4, 5)

# Calculate mean
mean_val <- mean(data)

# Calculate absolute deviations and MAD
mad <- mean(abs(data - mean_val))

print(mad)

Method 5: Using Statistical Software or Online Calculators

Finally, for those who prefer not to delve into programming or spreadsheet calculations, there are numerous statistical software packages and online calculators available that offer MAD calculation as one of their features. These tools usually require you to input your dataset and then provide the MAD along with other statistical measures.

💡 Note: When using any method, ensure that the dataset is correctly entered and that the chosen method aligns with the dataset's characteristics and the analysis's objectives.

In conclusion, calculating the Mean Absolute Deviation is a crucial step in understanding the variability within a dataset. By understanding and applying these five methods, data analysts and researchers can choose the most appropriate approach based on their dataset, computational resources, and personal preference. Whether through manual calculation, Excel, Python, R, or specialized software, calculating MAD provides valuable insights into the distribution of data, aiding in decision-making and further statistical analysis.