5 Ways To Find P Value

Introduction to P-Value
The p-value, or probability value, is a key concept in statistical hypothesis testing, representing the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. It is a crucial tool for determining the significance of a statistical test. The p-value helps researchers decide whether to reject the null hypothesis or fail to reject it, based on the data collected. In this article, we will explore five ways to find the p-value in different statistical scenarios.
Understanding P-Value
Before diving into the methods for finding the p-value, it’s essential to understand what the p-value represents. A small p-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, suggesting that the null hypothesis should be rejected in favor of the alternative hypothesis. On the other hand, a large p-value indicates that the data are consistent with the null hypothesis, and there is insufficient evidence to reject it.
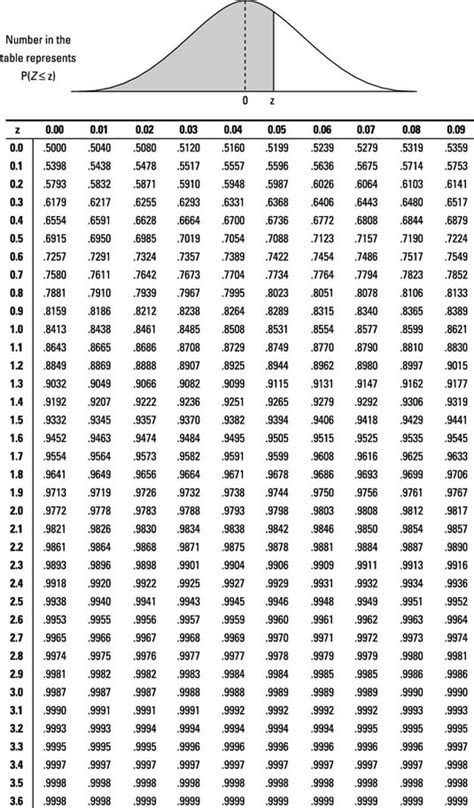
Method 1: Using a Z-Test

One common method for finding the p-value is by using a Z-test, which is applicable when the population standard deviation is known and the sample size is large. The Z-test statistic is calculated using the formula: Z = (X - μ) / (σ / √n), where X is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size. The p-value can then be found using a Z-table or a statistical calculator, looking up the Z-score to find the corresponding probability.
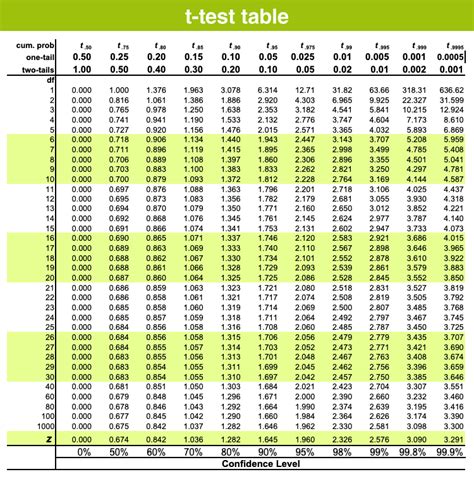
Method 2: Using a T-Test
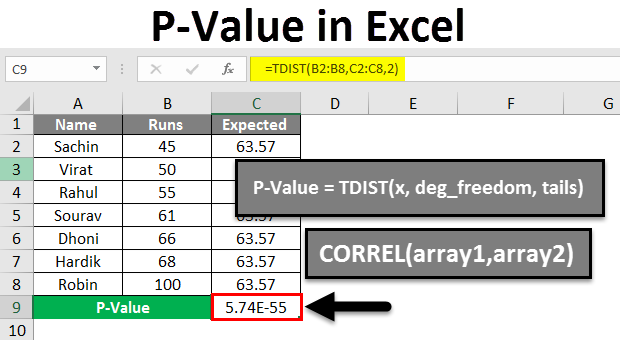
Another method for finding the p-value is by using a T-test, which is used when the population standard deviation is unknown or the sample size is small. Similar to the Z-test, the T-test statistic is calculated, but it takes into account the sample standard deviation (s) instead of the population standard deviation (σ). The formula for the T-test statistic is: t = (X - μ) / (s / √n). The p-value is then determined using a T-distribution table or a statistical software package, considering the degrees of freedom (n-1).
Method 3: Using ANOVA
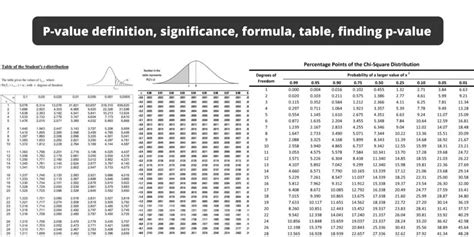
Analysis of Variance (ANOVA) is a statistical technique used to compare means of three or more samples. To find the p-value using ANOVA, the F-statistic is first calculated, which represents the ratio of the variance between groups to the variance within groups. The p-value associated with the F-statistic can be found using an F-distribution table or statistical software. A small p-value indicates that the means are significantly different, leading to the rejection of the null hypothesis that all means are equal.
Method 4: Using Non-Parametric Tests
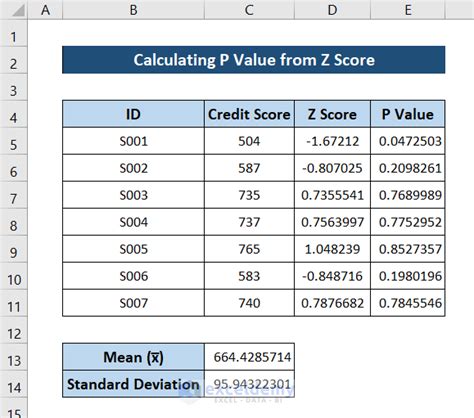
For data that do not meet the assumptions of parametric tests (such as normality), non-parametric tests can be used. These tests do not require a specific distribution of the data and are useful for ordinal data or when the data are not normally distributed. Examples include the Wilcoxon rank-sum test and the Kruskal-Wallis test. The p-value for non-parametric tests can often be found using statistical software, as the calculations can be complex and are typically not done by hand.
Method 5: Using Statistical Software
Finally, statistical software packages such as R, Python libraries (e.g., SciPy, Statsmodels), or SPSS can be used to find the p-value for various statistical tests. These programs can perform the calculations for Z-tests, T-tests, ANOVA, non-parametric tests, and more, providing the p-value directly. This method is the most efficient, especially for complex analyses or large datasets, as it minimizes the chance for human error in calculations.
📝 Note: Regardless of the method used, it's crucial to understand the assumptions of each test and ensure that the data meet these assumptions to interpret the p-value correctly.
To summarize, the choice of method for finding the p-value depends on the research question, the type of data, and the specific statistical test being used. Understanding the p-value and how to calculate it is essential for interpreting the results of statistical hypothesis tests.
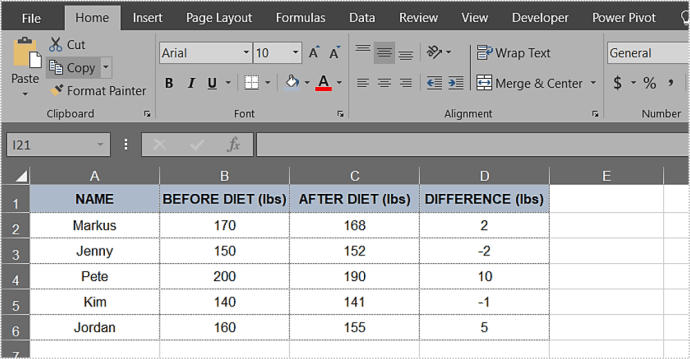
What does a small p-value indicate?
+
A small p-value indicates that the observed data would be very unlikely under the null hypothesis, suggesting that the null hypothesis should be rejected in favor of the alternative hypothesis.
What is the difference between a Z-test and a T-test?
+
The main difference is that a Z-test is used when the population standard deviation is known, whereas a T-test is used when the population standard deviation is unknown. The T-test also requires a smaller sample size compared to the Z-test.
How do I choose the correct statistical test for my data?
+
The choice of statistical test depends on the research question, the type of data (parametric or non-parametric), and whether the data meet the assumptions of the test. Consulting with a statistician or using statistical software can help in selecting the most appropriate test.
In the end, understanding and correctly applying statistical tests, including the calculation and interpretation of the p-value, is crucial for making informed decisions based on data analysis. Whether using traditional methods or statistical software, the p-value remains a fundamental tool in hypothesis testing, guiding researchers and analysts towards meaningful conclusions.