5 Ways To Do Square Root
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Calculating square roots is a fundamental mathematical operation that can be performed in various ways, including manually, using a calculator, or with the help of computational software. In this article, we will explore five different methods to calculate square roots, each with its own advantages and applications.
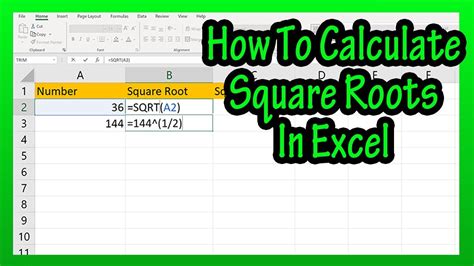
Method 1: Using a Calculator

One of the simplest and most straightforward ways to find the square root of a number is by using a calculator. Most calculators have a dedicated square root button, often denoted by the symbol √. To find the square root of a number using a calculator, simply enter the number and press the square root button. The result will be displayed on the screen. This method is quick, easy, and highly accurate, making it suitable for a wide range of applications, from basic arithmetic to complex mathematical calculations.
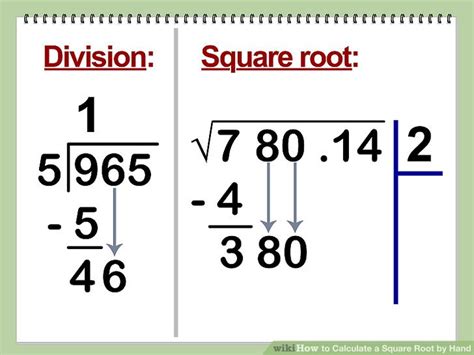
Method 2: Long Division Method
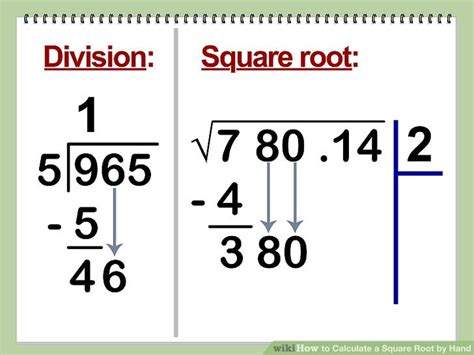
The long division method for finding square roots involves a series of steps that resemble long division. This method is particularly useful when calculating square roots manually without a calculator. Here’s how to do it: - Start by guessing the square root of the given number. - Divide the number by the guess. - Average the guess and the result of the division. - Use the average as a new guess and repeat the process until the desired level of precision is achieved. This method requires patience and practice but can be an effective way to calculate square roots manually.
Method 3: Prime Factorization
Another method to find the square root of a number involves prime factorization. This method is based on breaking down the number into its prime factors and then identifying pairs of the same prime factor. The square root of the number can be calculated by taking the product of the prime factors that appear in pairs. For example, to find the square root of 36: - Factorize 36 into its prime factors: 36 = 2 * 2 * 3 * 3. - Identify the pairs: (2 * 2) * (3 * 3). - Calculate the square root: √36 = √(2*2 * 3*3) = 2 * 3 = 6. This method is useful for numbers that can be easily factorized into their prime factors.
Method 4: Babylonian Method

The Babylonian method, also known as Heron’s method, is an ancient algorithm for computing the square root of a number. It is an iterative method that refines an initial guess for the square root. The formula for the Babylonian method is: [ x_{n+1} = \frac{1}{2}(x_n + \frac{S}{x_n}) ] where (S) is the number for which we are finding the square root, and (x_n) is the current estimate of the square root. This method converges very quickly and is used in many computational applications.
Method 5: Binary Search Method
The binary search method for finding square roots involves an iterative approach where we search for the square root within a defined range. Here’s a simplified outline: - Define a range within which the square root must lie. For a positive number (N), the range could be from 0 to (N). - Calculate the midpoint of the range. - Square the midpoint and compare it with (N). - If the square of the midpoint is less than (N), the square root must lie in the upper half of the range. If it is greater, the square root lies in the lower half. - Repeat the process with the new range until the desired precision is achieved. This method is efficient and can be easily implemented in programming languages for automated calculations.
📝 Note: Each of these methods has its own set of applications and suitability depending on the context, such as manual calculations, computational speed, or educational purposes.
In summary, calculating square roots can be approached in multiple ways, each with its unique characteristics and advantages. Whether it’s the simplicity of using a calculator, the educational value of the long division method, or the efficiency of computational algorithms like the Babylonian method, understanding these different approaches can enhance one’s mathematical toolkit and problem-solving capabilities. By mastering these methods, individuals can tackle a wide range of mathematical and real-world problems with confidence and precision.
What is the most accurate method for calculating square roots?
+
The most accurate method often depends on the tools available and the context of the calculation. For manual calculations, the long division method or prime factorization can be very accurate. However, for computational purposes, algorithms like the Babylonian method provide high accuracy and efficiency.
How do calculators calculate square roots so quickly?
+
Calculators use specialized algorithms and mathematical libraries that are optimized for speed and accuracy. These algorithms can include variations of the Babylonian method, logarithmic methods, or other computational techniques that are designed to produce results quickly and accurately.
What are the practical applications of calculating square roots?

+
Calculating square roots has numerous practical applications across various fields, including physics, engineering, economics, and computer science. It is used in calculations involving distances, velocities, frequencies, and in solving quadratic equations, among many other applications.