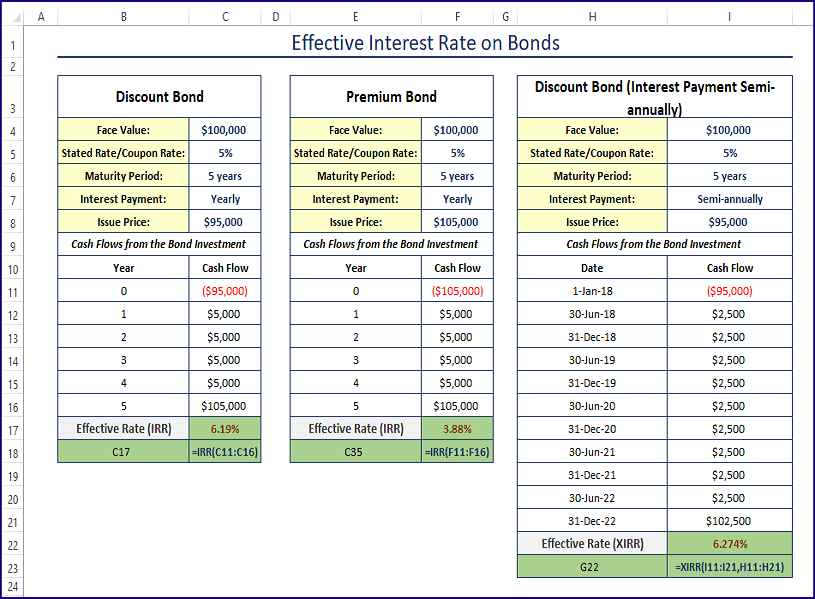
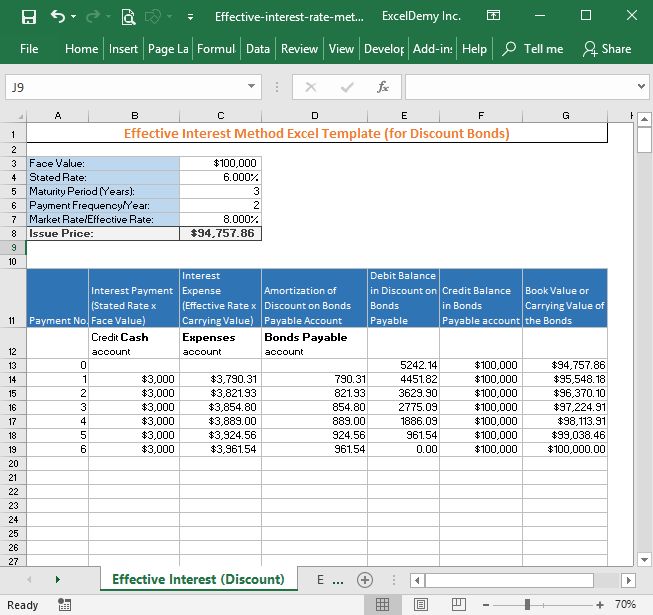
Compute Effective Interest Rate In Excel
Introduction to Effective Interest Rate
The effective interest rate is a crucial concept in finance that represents the actual interest rate earned on an investment or paid on a loan over a year, taking into account the compounding effect. It is essential to understand how to compute the effective interest rate in Excel, as it helps in making informed decisions about investments and loans. In this article, we will explore the concept of the effective interest rate, its importance, and how to calculate it using Excel.
Understanding Effective Interest Rate

The effective interest rate is different from the nominal interest rate, which is the rate quoted by lenders or investors. The nominal interest rate does not take into account the compounding effect, which can significantly impact the actual interest earned or paid. The effective interest rate, on the other hand, considers the compounding effect, providing a more accurate picture of the interest earned or paid over a year.
Formula to Calculate Effective Interest Rate

The formula to calculate the effective interest rate is: [ (1 + \frac{r}{n})^n - 1 ] where: - ( r ) is the nominal interest rate, - ( n ) is the number of compounding periods per year.
Calculating Effective Interest Rate in Excel
To calculate the effective interest rate in Excel, you can use the following steps:
- Enter the nominal interest rate in a cell, for example, A1.
- Enter the number of compounding periods per year in another cell, for example, B1.
- Use the formula: ( = (1 + A1/B1)^{B1} - 1 ) to calculate the effective interest rate.
- Press Enter to get the result.
For example, if the nominal interest rate is 6% and the interest is compounded monthly, the formula would be: [ = (1 + 0.06/12)^{12} - 1 ]
This will give you the effective interest rate, which you can format as a percentage.
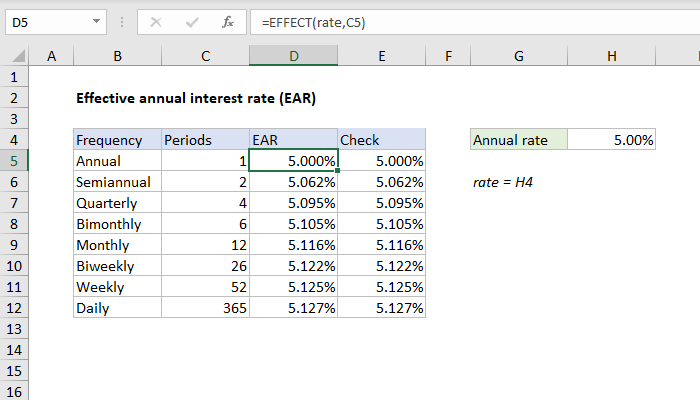
Using the EFFECT Function in Excel
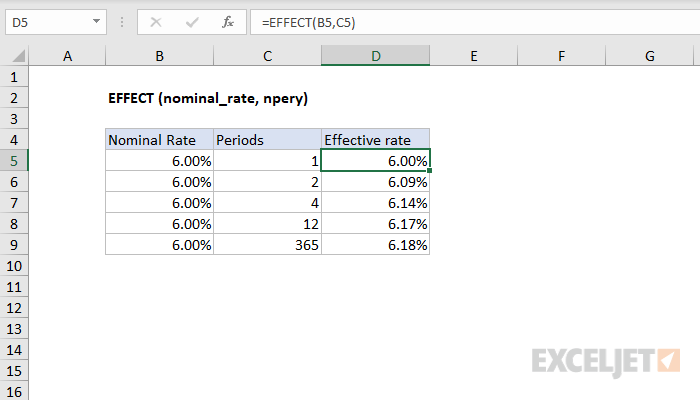
Excel provides a built-in function called EFFECT, which can be used to calculate the effective interest rate. The syntax of the EFFECT function is: [ \text{EFFECT}(\text{nominal_rate}, \text{compounding_frequency}) ]
where: - nominal_rate is the nominal interest rate, - compounding_frequency is the number of compounding periods per year.
Using the same example as above, the EFFECT function would be: [ = \text{EFFECT}(0.06, 12) ]
This will give you the effective interest rate, which you can format as a percentage.
Importance of Effective Interest Rate
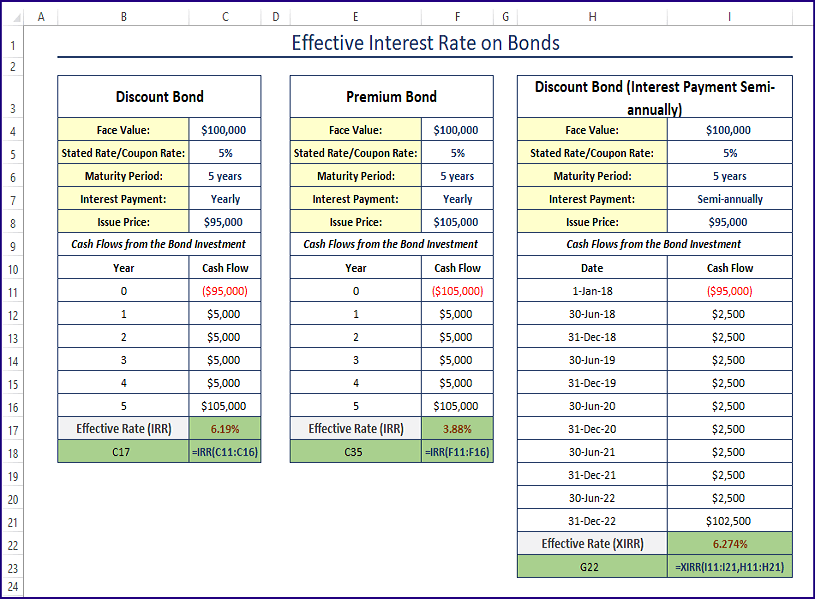
The effective interest rate is essential in finance because it provides a more accurate picture of the interest earned or paid over a year. It helps investors and borrowers make informed decisions about investments and loans. For example, when comparing two loans with different nominal interest rates and compounding frequencies, the effective interest rate can help determine which loan is more expensive.
Examples of Effective Interest Rate
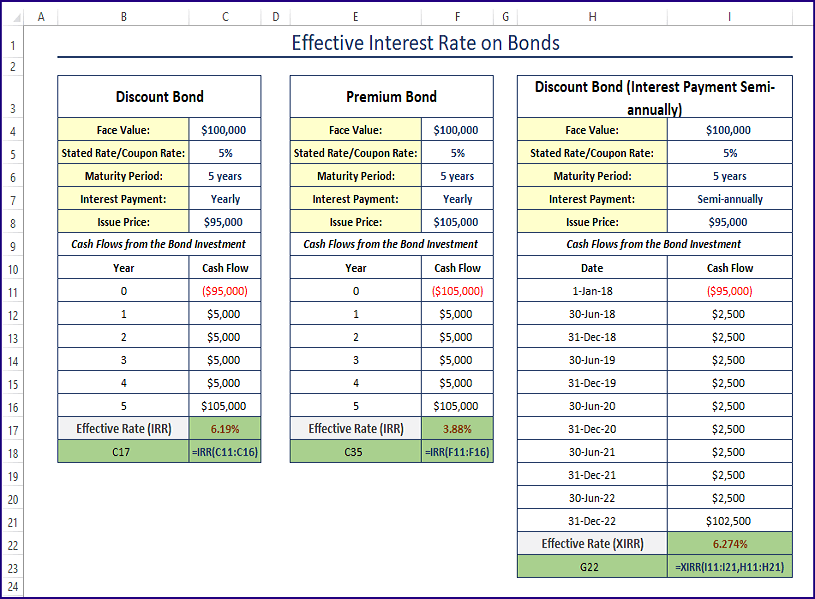
Here are a few examples of effective interest rate calculations:
- Nominal interest rate: 5%, compounded monthly. Effective interest rate: ( = (1 + 0.05/12)^{12} - 1 ) = 5.12%
- Nominal interest rate: 7%, compounded quarterly. Effective interest rate: ( = (1 + 0.07/4)^4 - 1 ) = 7.19%
- Nominal interest rate: 4%, compounded annually. Effective interest rate: ( = (1 + 0.04/1)^1 - 1 ) = 4.00%
As you can see, the effective interest rate can be significantly different from the nominal interest rate, especially when the compounding frequency is high.
Table of Effective Interest Rates
The following table shows the effective interest rates for different nominal interest rates and compounding frequencies:
| Nominal Interest Rate | Compounding Frequency | Effective Interest Rate |
|---|---|---|
| 5% | Monthly | 5.12% |
| 7% | Quarterly | 7.19% |
| 4% | Annually | 4.00% |
📝 Note: The effective interest rate calculations in this article assume that the interest is compounded at the specified frequency, and that the nominal interest rate remains constant over the year.
To summarize, the effective interest rate is a crucial concept in finance that represents the actual interest rate earned on an investment or paid on a loan over a year. It is essential to understand how to compute the effective interest rate in Excel, as it helps in making informed decisions about investments and loans. By using the formula or the EFFECT function in Excel, you can calculate the effective interest rate and make more accurate decisions.
What is the difference between nominal and effective interest rate?

+
The nominal interest rate is the rate quoted by lenders or investors, while the effective interest rate is the actual interest rate earned or paid over a year, taking into account the compounding effect.
How do I calculate the effective interest rate in Excel?
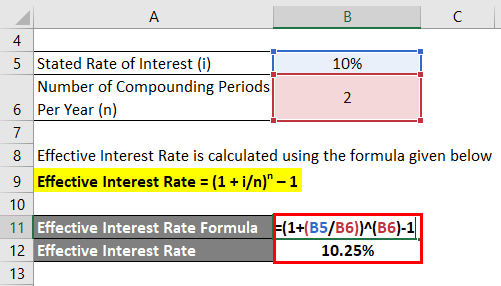
+
You can calculate the effective interest rate in Excel using the formula: ( = (1 + A1/B1)^{B1} - 1 ) or by using the EFFECT function: ( = \text{EFFECT}(A1, B1) ), where A1 is the nominal interest rate and B1 is the number of compounding periods per year.
Why is the effective interest rate important in finance?

+
The effective interest rate is essential in finance because it provides a more accurate picture of the interest earned or paid over a year, helping investors and borrowers make informed decisions about investments and loans.