Calculate P Value In Excel

Introduction to P-Value Calculation in Excel
When working with statistical data in Excel, calculating the p-value is a crucial step in determining the significance of your results. The p-value, or probability value, is a key concept in hypothesis testing, indicating the probability of observing your results (or more extreme) given that the null hypothesis is true. In this blog post, we will delve into the world of p-value calculation in Excel, exploring the different methods and functions available to help you make informed decisions about your data.
Understanding P-Value
Before we dive into the calculation process, it’s essential to understand what a p-value represents. The p-value is a numerical value between 0 and 1 that indicates the probability of observing your results (or more extreme) assuming that the null hypothesis is true. A small p-value (typically less than 0.05) suggests that the observed results are unlikely to occur by chance, leading to the rejection of the null hypothesis. On the other hand, a large p-value indicates that the results are likely due to chance, and the null hypothesis cannot be rejected.
Calculating P-Value in Excel
Excel provides several functions to calculate the p-value, depending on the type of test you want to perform. Here are a few common methods:
- T-Test: The T-Test is a popular statistical test used to compare the means of two groups. To calculate the p-value using the T-Test, you can use the
T.TESTfunction in Excel. The syntax isT.TEST(array1, array2, tails, type), wherearray1andarray2are the ranges of data,tailsspecifies the number of tails (1 or 2), andtypespecifies the type of test (1 for paired, 2 for unpaired). - Z-Test: The Z-Test is another statistical test used to compare the means of two groups. To calculate the p-value using the Z-Test, you can use the
Z.TESTfunction in Excel. The syntax isZ.TEST(array1, array2, tails), wherearray1andarray2are the ranges of data, andtailsspecifies the number of tails (1 or 2). - ANOVA: The ANOVA (Analysis of Variance) test is used to compare the means of multiple groups. To calculate the p-value using ANOVA, you can use the
ANOVAfunction in Excel. The syntax isANOVA(range, group_range, alpha), whererangeis the range of data,group_rangeis the range of group labels, andalphais the significance level.
Example Calculations

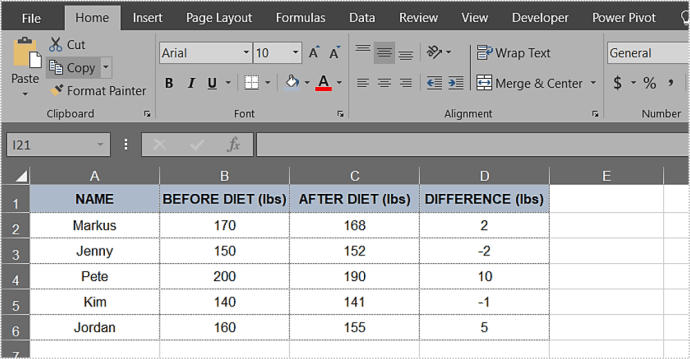
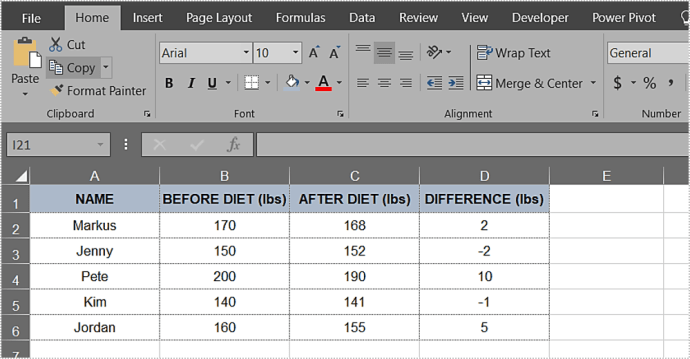
Let’s consider an example to illustrate the calculation of p-value in Excel. Suppose we want to compare the average scores of two groups of students. We have the following data:
| Group A | Group B |
|---|---|
| 85 | 78 |
| 90 | 82 |
| 78 | 85 |
| 92 | 88 |
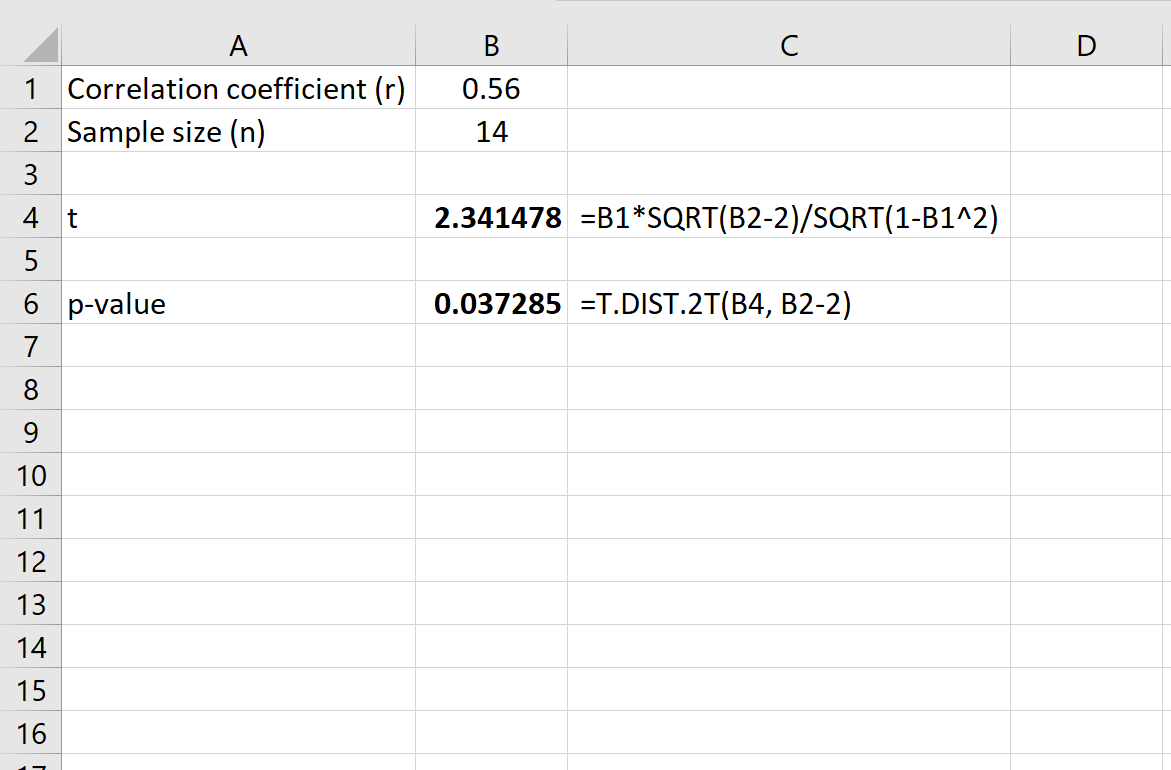
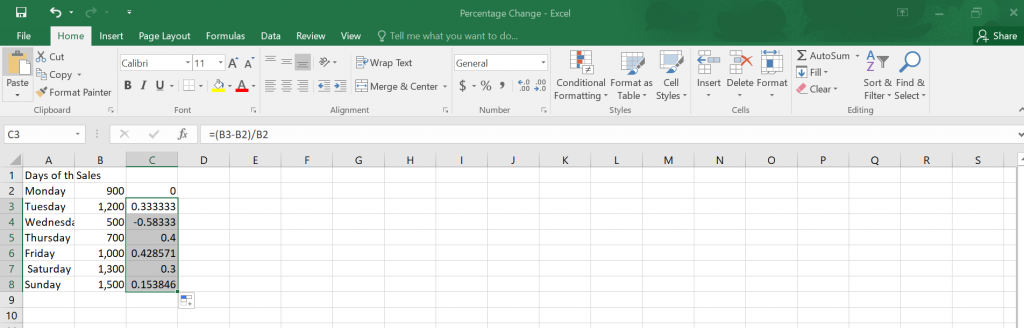
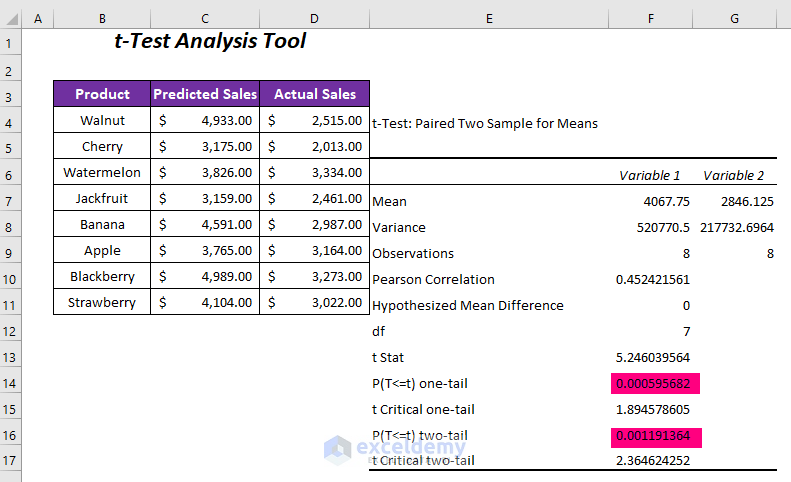
To calculate the p-value using the T-Test, we can use the following formula: =T.TEST(A1:A4, B1:B4, 2, 2), where A1:A4 and B1:B4 are the ranges of data for Group A and Group B, respectively. The result will give us the p-value, which we can use to determine the significance of the results.
📝 Note: The `T.TEST` function assumes that the data is normally distributed and that the variances are equal. If these assumptions are not met, alternative tests such as the Wilcoxon rank-sum test or the Welch's t-test may be more appropriate.
Interpreting P-Value Results

Once we have calculated the p-value, we need to interpret the results. A small p-value (typically less than 0.05) indicates that the observed results are unlikely to occur by chance, and we can reject the null hypothesis. On the other hand, a large p-value indicates that the results are likely due to chance, and we cannot reject the null hypothesis.
Here are some general guidelines for interpreting p-value results:
- p-value < 0.05: Reject the null hypothesis (the results are statistically significant)
- p-value > 0.05: Fail to reject the null hypothesis (the results are not statistically significant)
- p-value = 0.05: The results are marginally significant (the p-value is exactly equal to the significance level)
Conclusion and Future Directions

In conclusion, calculating the p-value in Excel is a straightforward process using the various functions available. By understanding the concept of p-value and how to interpret the results, we can make informed decisions about our data and draw meaningful conclusions. As we continue to work with statistical data, it’s essential to remember that the p-value is just one aspect of statistical analysis, and we should consider other factors such as sample size, data distribution, and study design when interpreting the results.
What is the difference between a one-tailed and two-tailed test?
+
A one-tailed test is used to determine if there is a significant difference between the means of two groups in a specific direction (e.g., Group A is greater than Group B). A two-tailed test, on the other hand, is used to determine if there is a significant difference between the means of two groups in either direction (e.g., Group A is greater than or less than Group B).
How do I choose the correct significance level for my test?

+
The choice of significance level depends on the research question and the level of risk you are willing to take. A common significance level is 0.05, which means that there is a 5% chance of rejecting the null hypothesis when it is true. However, you may choose a more stringent significance level (e.g., 0.01) or a more lenient significance level (e.g., 0.10) depending on your research goals.
Can I use the p-value to determine the effect size of my results?
+
No, the p-value does not provide information about the effect size of your results. The p-value only indicates the probability of observing your results (or more extreme) given that the null hypothesis is true. To determine the effect size, you need to calculate additional statistics such as the mean difference or the correlation coefficient.