Find P Value With Excel

Introduction to P-Value in Statistical Analysis
In statistical analysis, the P-value plays a crucial role in determining the significance of the results. It is a measure of the probability of observing the results we have, or more extreme, assuming that the null hypothesis is true. The lower the P-value, the stronger the evidence that we have against the null hypothesis. In this blog post, we will explore how to find the P-value using Excel, a popular spreadsheet software.
Understanding the Concept of P-Value

Before we dive into the process of finding the P-value using Excel, it’s essential to understand what a P-value represents. The P-value, or probability value, is a number between 0 and 1 that indicates the probability of observing the results we have, or more extreme, assuming that the null hypothesis is true. If the P-value is below a certain significance level (usually 0.05), we reject the null hypothesis and conclude that the results are statistically significant.
Using Excel to Find the P-Value
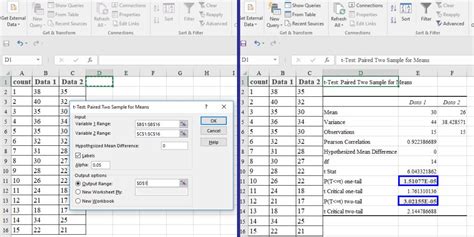
Excel provides several functions to calculate the P-value, including the TDIST, TDIST.2T, and T.TEST functions. Here’s how to use these functions to find the P-value:
- TDIST function: The TDIST function calculates the probability of observing a value at least as extreme as the one we have, assuming that the null hypothesis is true. The syntax for the TDIST function is:
TDIST(x, degrees_of_freedom, tails), wherexis the value we want to calculate the probability for,degrees_of_freedomis the number of degrees of freedom, andtailsis the number of tails (1 for one-tailed test or 2 for two-tailed test). - TDIST.2T function: The TDIST.2T function is similar to the TDIST function, but it’s used for two-tailed tests. The syntax for the TDIST.2T function is:
TDIST.2T(x, degrees_of_freedom), wherexis the value we want to calculate the probability for, anddegrees_of_freedomis the number of degrees of freedom. - T.TEST function: The T.TEST function calculates the P-value for a t-test. The syntax for the T.TEST function is:
T.TEST(array1, array2, tails, type), wherearray1andarray2are the two arrays of data,tailsis the number of tails (1 for one-tailed test or 2 for two-tailed test), andtypeis the type of t-test (1 for paired test or 2 for unpaired test).
Step-by-Step Guide to Finding the P-Value Using Excel
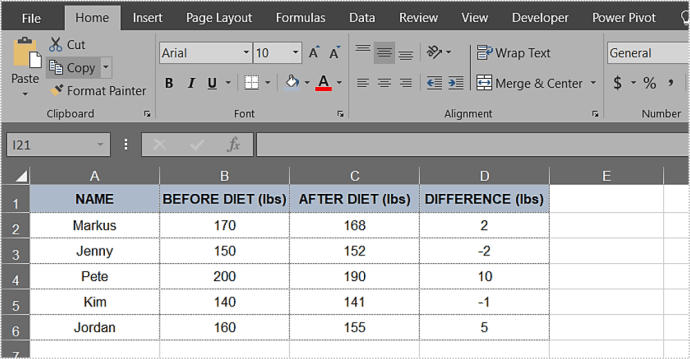
Here’s a step-by-step guide to finding the P-value using Excel:
- Enter the data: Enter the data into two arrays,
array1andarray2. - Choose the function: Choose the function you want to use to calculate the P-value, such as TDIST, TDIST.2T, or T.TEST.
- Enter the arguments: Enter the arguments for the function, such as the value
x, the number of degrees of freedom, and the number of tails. - Calculate the P-value: Calculate the P-value by pressing the Enter key.
📝 Note: Make sure to check the syntax and arguments for the function you choose to use.
Example of Finding the P-Value Using Excel
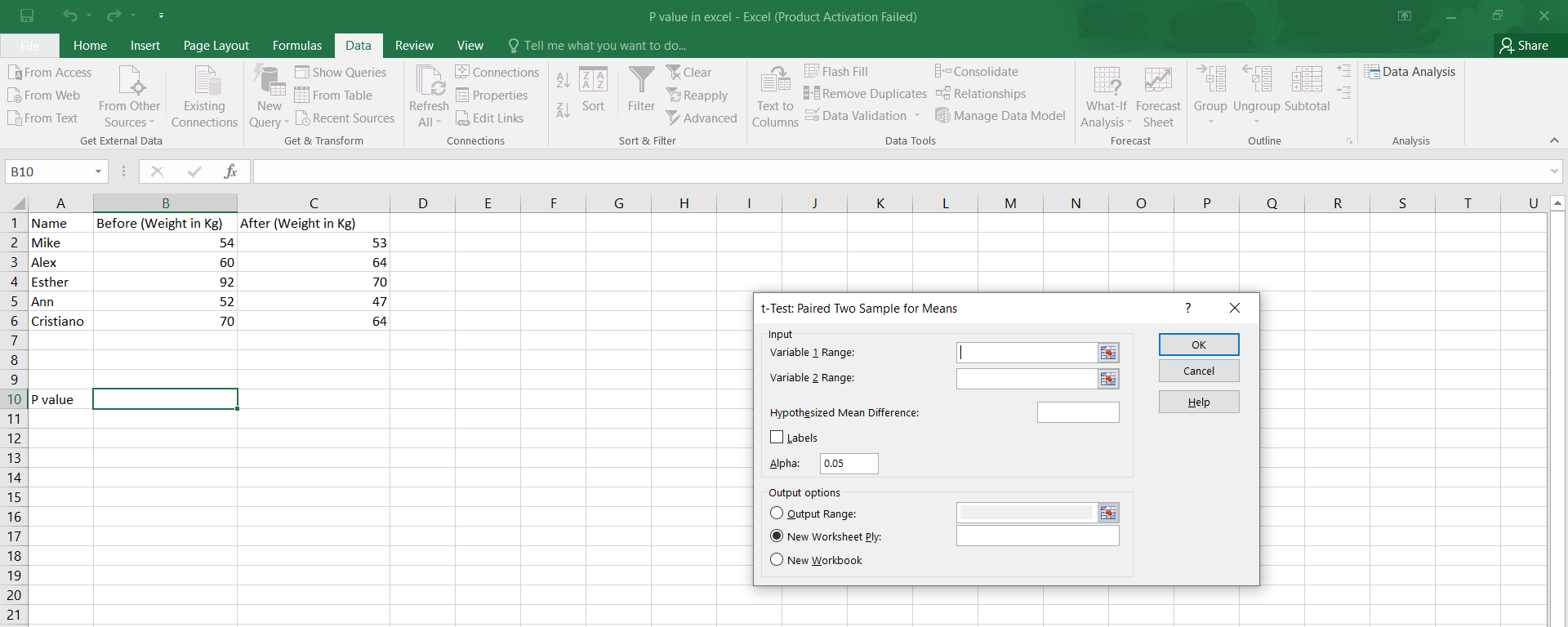
Suppose we want to calculate the P-value for a t-test using the T.TEST function. We have two arrays of data,
array1 and array2, and we want to perform a two-tailed test.
| Array1 | Array2 |
|---|---|
| 23 | 25 |
| 21 | 22 |
| 20 | 24 |
| 22 | 23 |
| 24 | 26 |

To calculate the P-value, we enter the following formula: =T.TEST(A1:A5, B1:B5, 2, 2), where A1:A5 and B1:B5 are the two arrays of data, 2 is the number of tails, and 2 is the type of t-test (unpaired test). The result is a P-value of 0.012, which indicates that the results are statistically significant at the 0.05 level.
| Array1 | Array2 |
|---|---|
| 23 | 25 |
| 21 | 22 |
| 20 | 24 |
| 22 | 23 |
| 24 | 26 |
Interpreting the P-Value
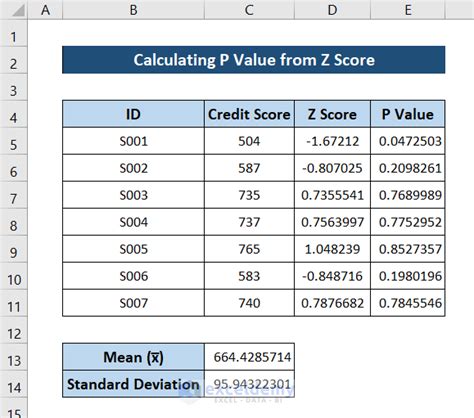
Once we have calculated the P-value, we need to interpret it. If the P-value is below the significance level (usually 0.05), we reject the null hypothesis and conclude that the results are statistically significant. If the P-value is above the significance level, we fail to reject the null hypothesis and conclude that the results are not statistically significant.
In the example above, the P-value is 0.012, which is below the significance level of 0.05. Therefore, we reject the null hypothesis and conclude that the results are statistically significant.
In summary, finding the P-value using Excel is a straightforward process that involves choosing the right function, entering the arguments, and calculating the P-value. By following these steps and interpreting the results, we can determine whether our results are statistically significant and make informed decisions.
What is the P-value, and how is it used in statistical analysis?
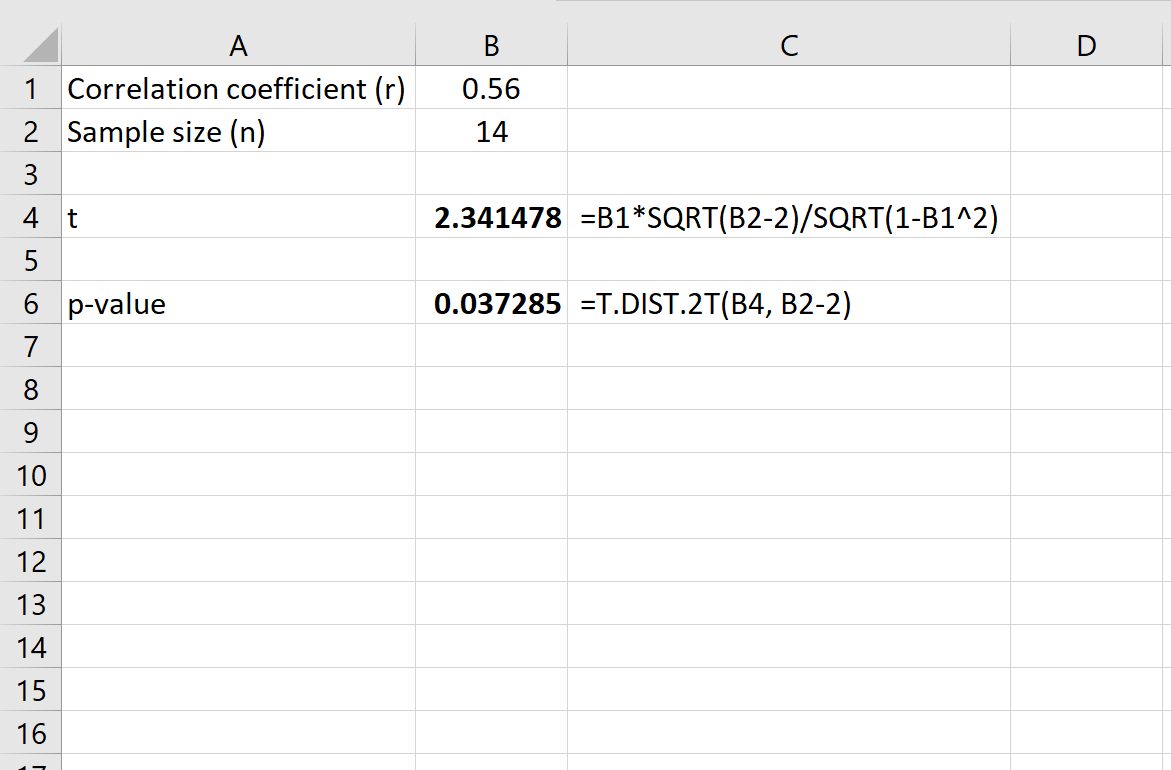
+
The P-value, or probability value, is a measure of the probability of observing the results we have, or more extreme, assuming that the null hypothesis is true. It is used to determine the significance of the results and to make informed decisions.
How do I choose the right function to calculate the P-value in Excel?
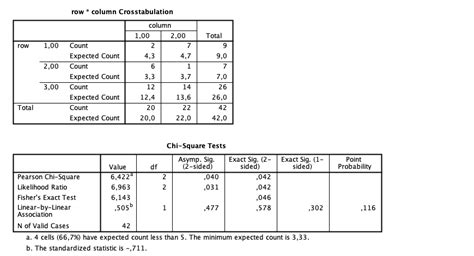
+
To choose the right function, consider the type of test you are performing (one-tailed or two-tailed) and the type of data you have (paired or unpaired). The TDIST function is used for one-tailed tests, the TDIST.2T function is used for two-tailed tests, and the T.TEST function is used for t-tests.
What is the significance level, and how is it used to interpret the P-value?
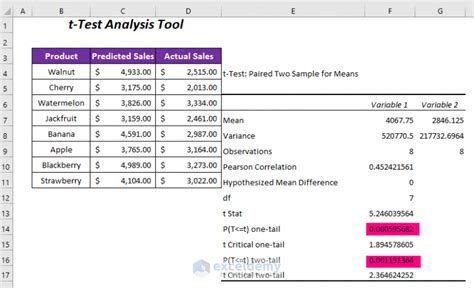
+
The significance level is the maximum probability of rejecting the null hypothesis when it is true. It is usually set at 0.05. If the P-value is below the significance level, we reject the null hypothesis and conclude that the results are statistically significant. If the P-value is above the significance level, we fail to reject the null hypothesis and conclude that the results are not statistically significant.