5 Ways To Anova
Introduction to Anova

Analysis of Variance, commonly referred to as Anova, is a statistical technique used to compare means of two or more samples to find out if at least one of the means is different. It is a powerful tool for analyzing and understanding complex data sets, helping researchers and analysts to make informed decisions. In this article, we will delve into the world of Anova, exploring its applications, benefits, and the different types of Anova tests available.
What is Anova?

Anova is based on the concept of variance, which measures the dispersion of a set of data points. By comparing the variance between groups to the variance within groups, Anova determines if the difference between the groups is due to chance or if there is a statistically significant difference. This technique is widely used in various fields, including business, medicine, social sciences, and engineering, to analyze and interpret data from experiments, surveys, and observational studies.
Types of Anova

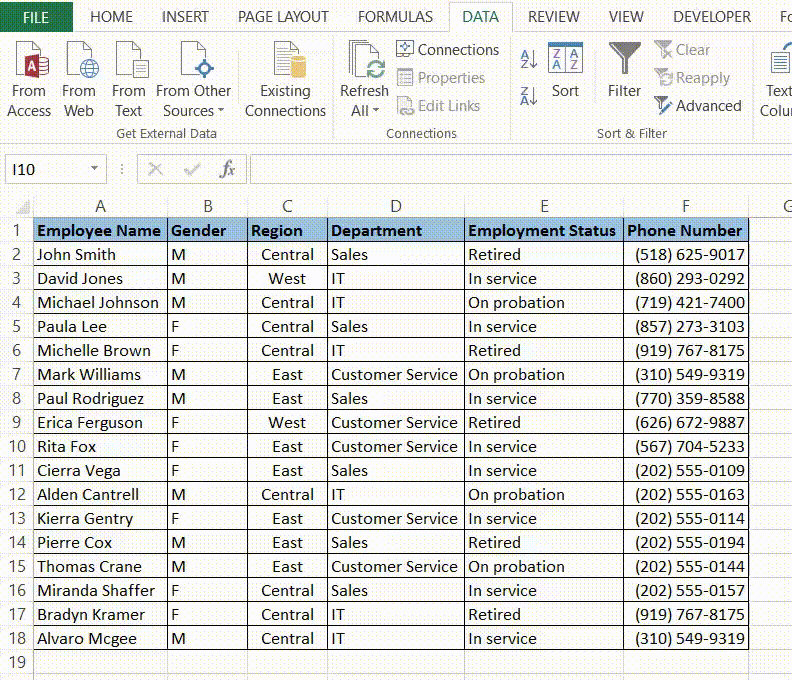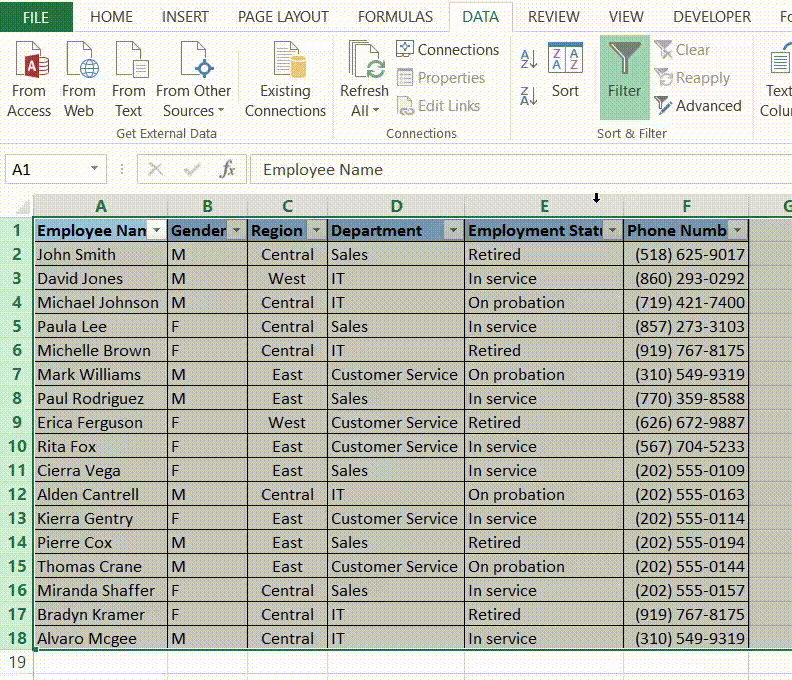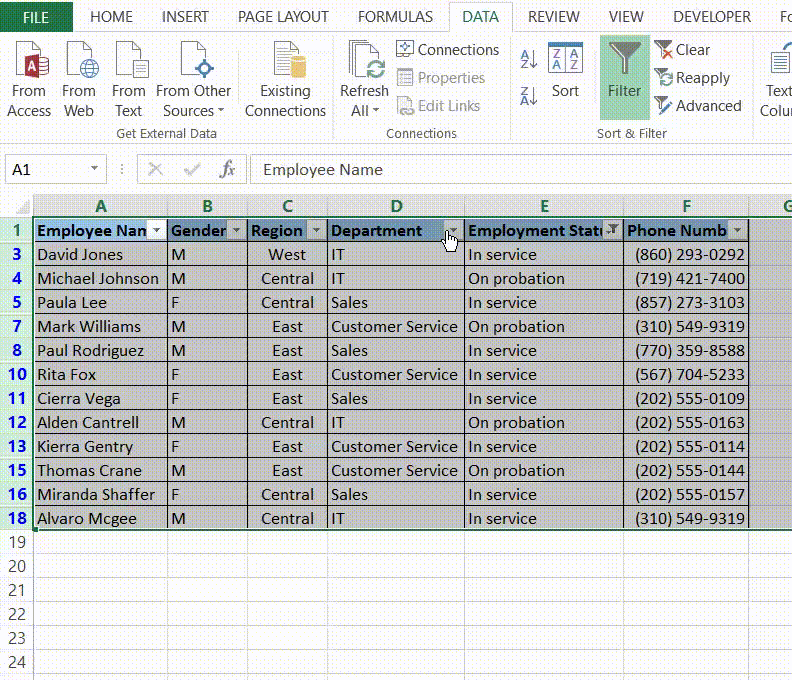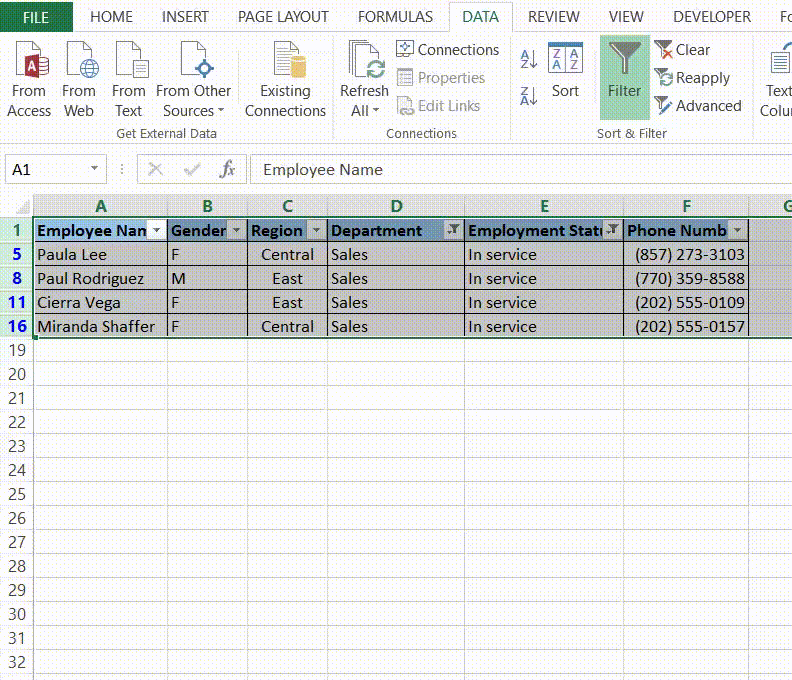
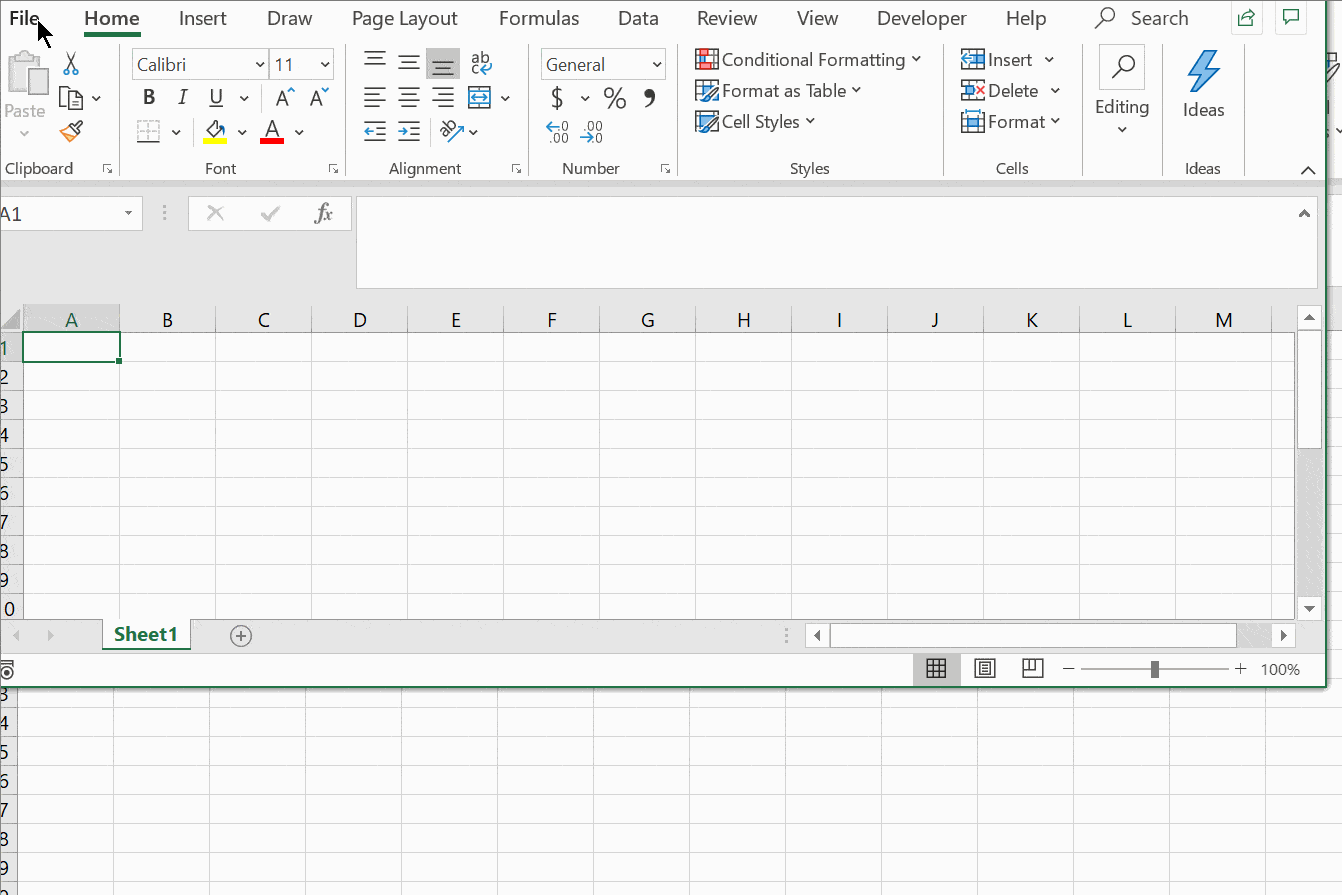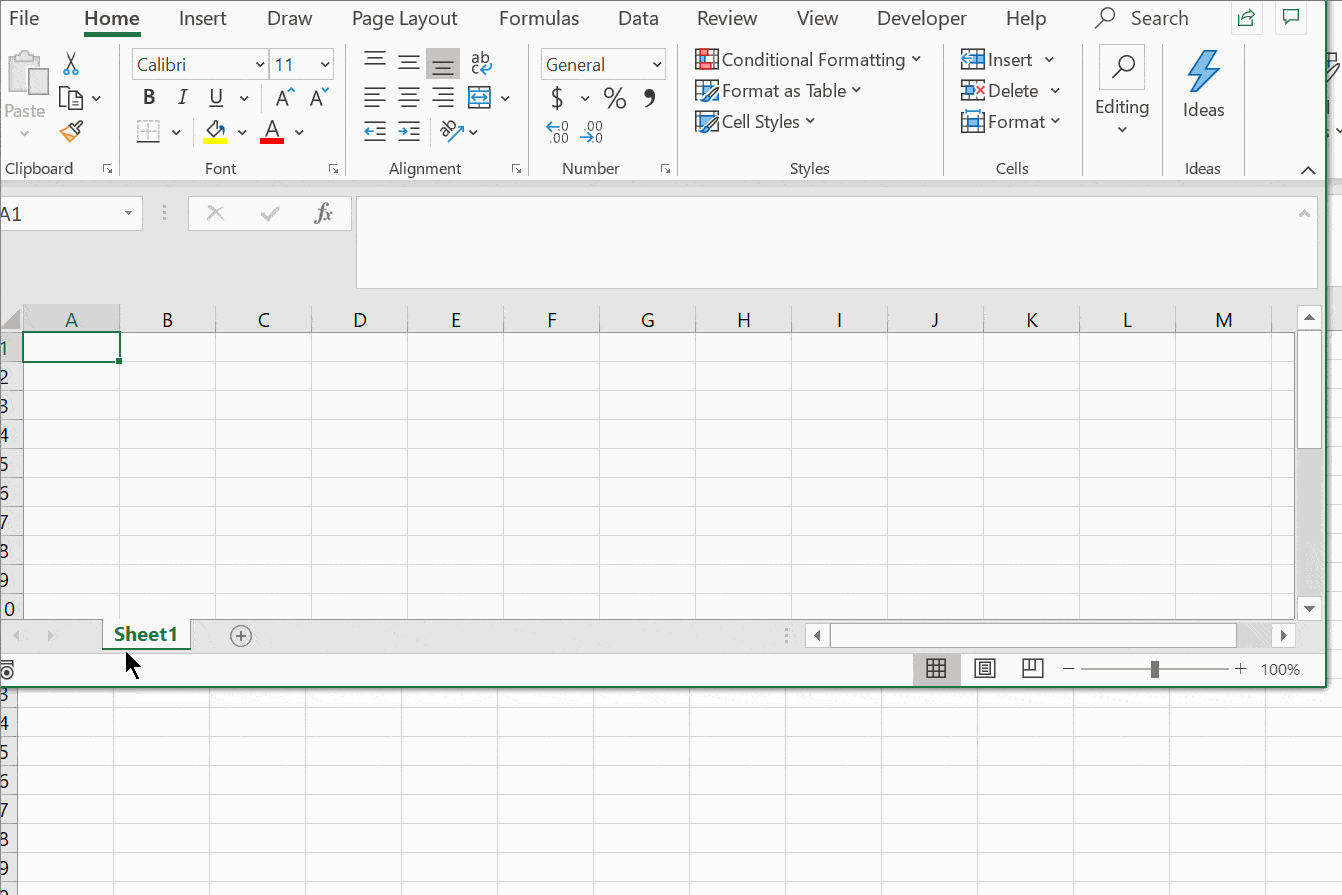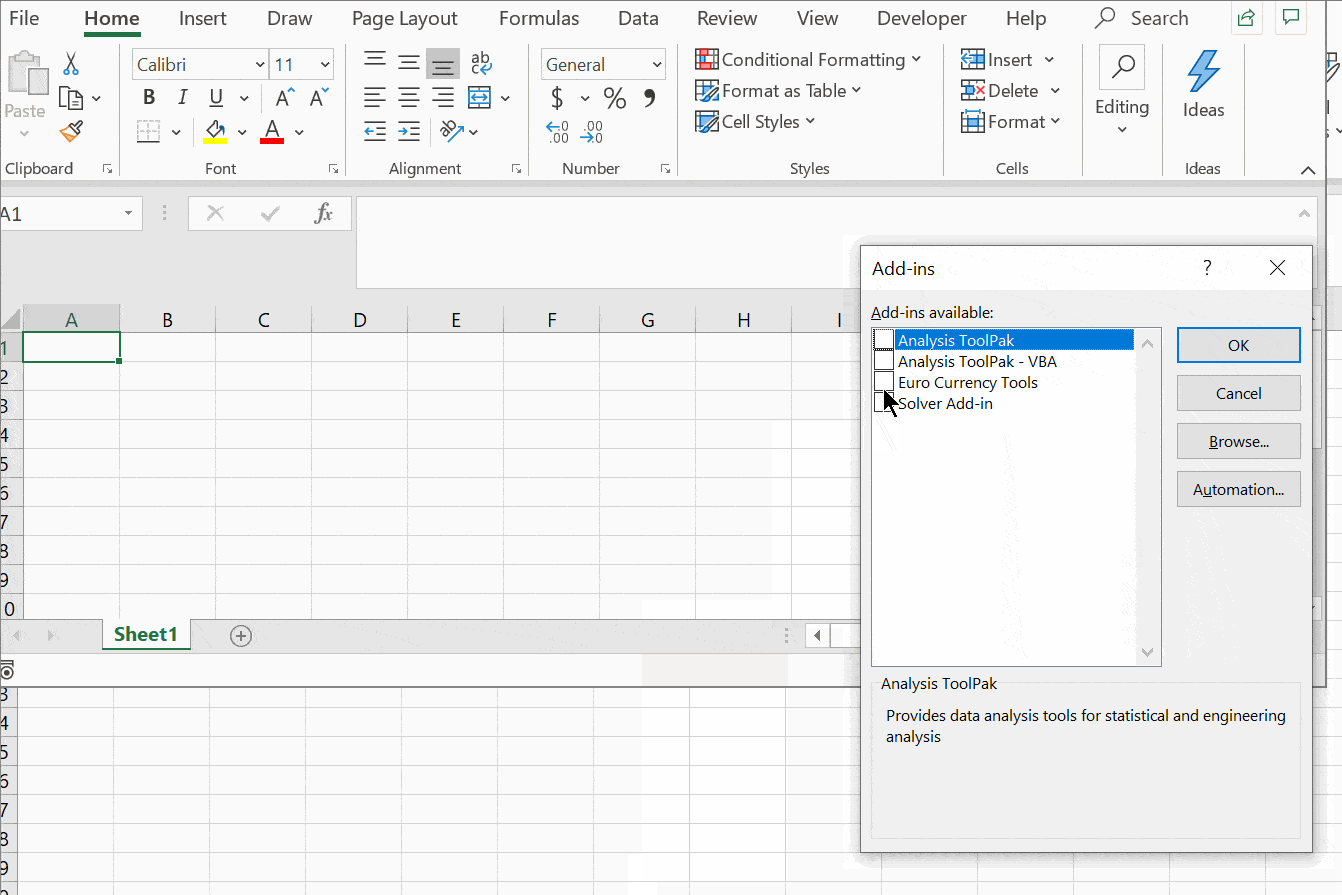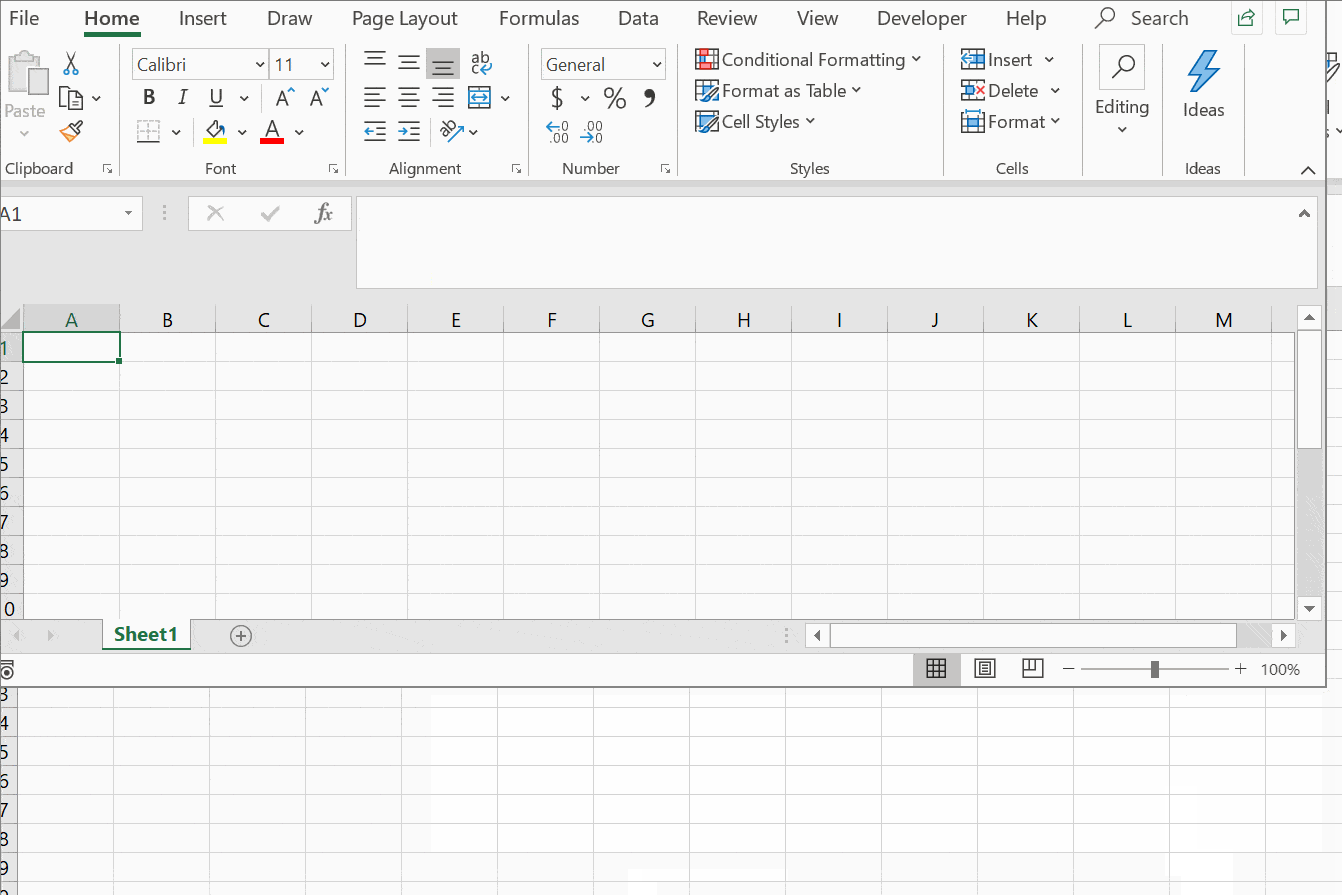
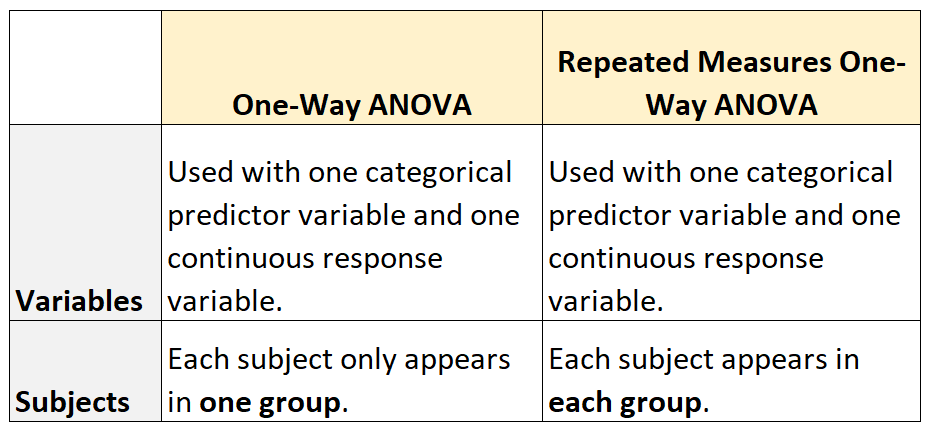
There are several types of Anova tests, each designed to address specific research questions and data characteristics. Here are five common types of Anova: * One-Way Anova: Used to compare the means of two or more groups to determine if there is a significant difference between them. * Two-Way Anova: Examines the effect of two independent variables on a continuous dependent variable, allowing for the interaction between the independent variables to be assessed. * N-Way Anova: An extension of the two-way Anova, this type of analysis involves more than two independent variables and is used to study the effects of multiple factors on a dependent variable. * Repeated Measures Anova: Used when the same subjects are measured under different conditions or at different times, this type of Anova accounts for the correlation between the repeated measures. * Mixed Anova: Combines elements of both between-subjects and within-subjects designs, allowing for the analysis of data with both fixed and random effects.
Applications of Anova
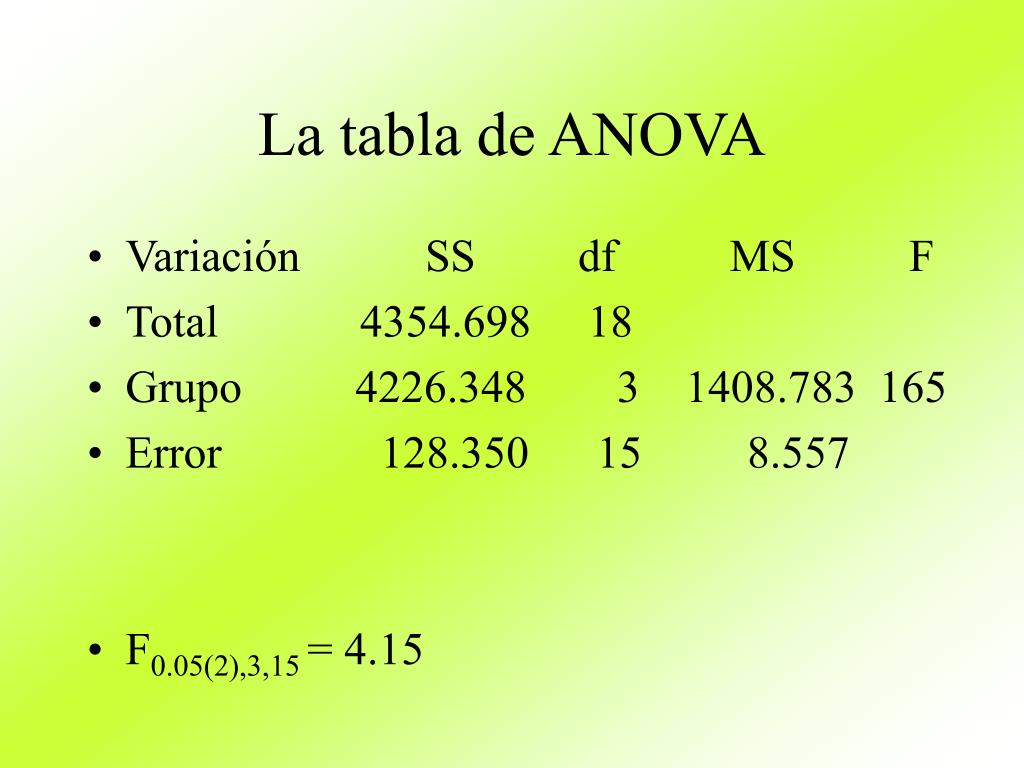
The applications of Anova are diverse and widespread, reflecting the technique’s versatility and power. Some examples include: * Quality Control: Anova is used in manufacturing to compare the quality of products from different production lines or to evaluate the effect of different materials on product quality. * Medical Research: Anova is applied in clinical trials to compare the efficacy of different treatments or to assess the impact of various factors on patient outcomes. * Marketing Research: Anova helps marketers to understand consumer behavior, comparing the preferences and buying habits of different demographic groups. * Agricultural Research: Anova is used to compare the yields of different crop varieties, the effects of fertilizers, or the impact of climate change on agricultural productivity.
Benefits of Anova
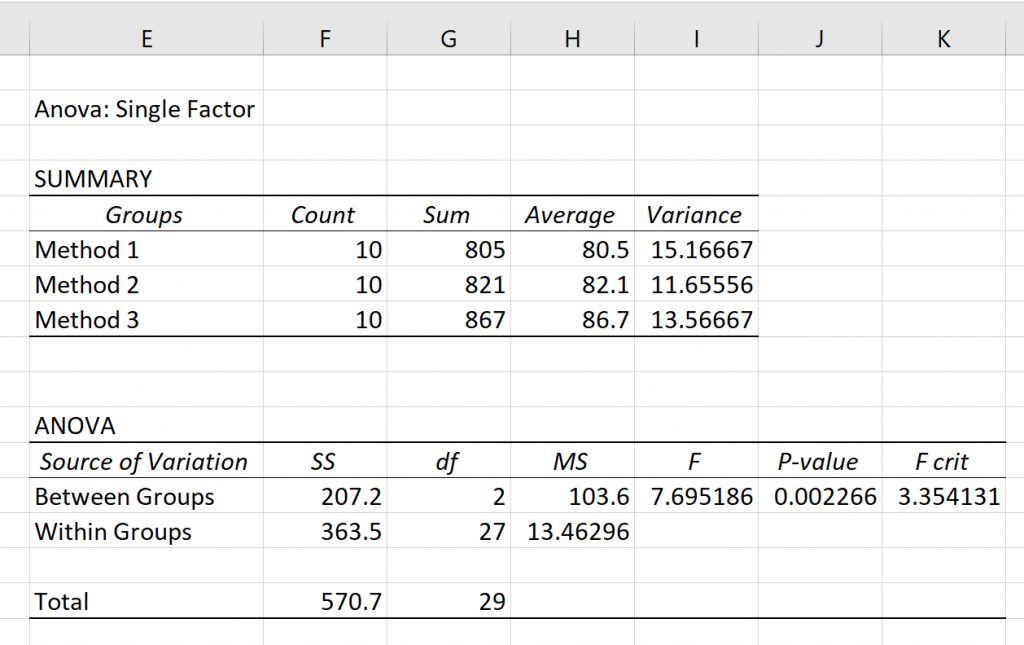
The benefits of using Anova include: * Statistical Significance: Anova provides a statistical measure of whether the observed differences between groups are due to chance or if they reflect a real effect. * Comparison of Multiple Groups: Anova allows for the simultaneous comparison of more than two groups, which is more efficient and powerful than performing multiple t-tests. * Flexibility: Anova can be applied to a wide range of data types and experimental designs, making it a versatile tool for data analysis. * Ease of Interpretation: The results of Anova tests are relatively straightforward to interpret, providing clear indications of whether differences between groups are statistically significant.
📝 Note: It is essential to ensure that the data meet the assumptions of Anova, including normality, homogeneity of variance, and independence of observations, to guarantee the validity of the results.
Conclusion and Future Directions
In conclusion, Anova is a powerful statistical technique with a broad range of applications across various disciplines. Its ability to compare means, assess the significance of differences, and analyze complex data sets makes it an indispensable tool for researchers and analysts. As data analysis continues to evolve, the development of new Anova methodologies and the integration of Anova with other statistical techniques will further enhance its utility and impact.
What is the main purpose of Anova?

+
The main purpose of Anova is to compare the means of two or more samples to determine if at least one of the means is different, helping to understand if the observed differences are due to chance or if they reflect a real effect.
What are the assumptions of Anova?

+
The assumptions of Anova include normality of the residuals, homogeneity of variance (or homoscedasticity), and independence of observations. Ensuring these assumptions are met is crucial for the validity of Anova results.
Can Anova be used for non-parametric data?

+
While Anova is primarily used for parametric data, there are non-parametric alternatives, such as the Kruskal-Wallis test, which can be used when the data do not meet the assumptions of Anova. These tests are based on ranks rather than the actual data values.