5 Ways To Determine P Value

Introduction to P-Value

The P-value, or probability value, is a key concept in statistical hypothesis testing, representing the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. The calculation and interpretation of P-values are crucial in determining the significance of the results in various fields, including medicine, social sciences, and physics. In this article, we will explore five ways to determine the P-value, understanding its significance, and how it applies to different scenarios.

Understanding P-Value

Before diving into the methods of determining the P-value, it’s essential to understand what it signifies. A small P-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, leading to the rejection of the null hypothesis. On the other hand, a large P-value suggests that the data are consistent with the null hypothesis, and there is not enough evidence to reject it. The choice of the significance level (alpha) affects the decision; commonly, alpha is set to 0.05.

Methods to Determine P-Value

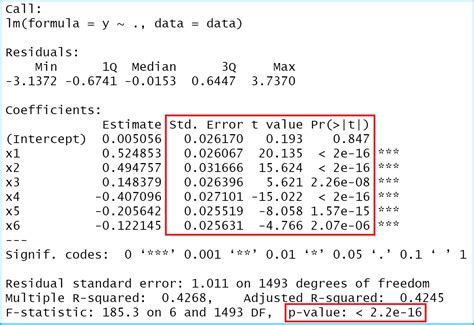
There are several methods to calculate the P-value, depending on the type of data, the hypothesis being tested, and the statistical test used. Here are five common methods:

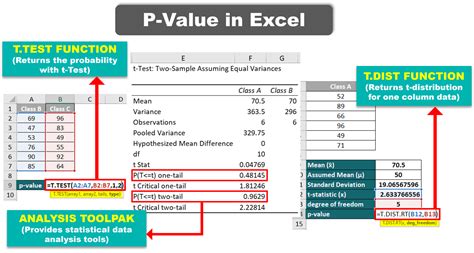
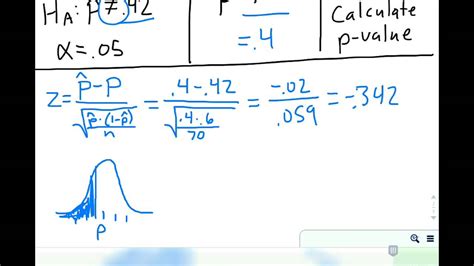
• 1. Using a Z-Test or T-Test: For comparing the mean of a sample to a known population mean or for comparing the means of two samples, Z-tests and T-tests are commonly used. The P-value can be calculated using the test statistic and the degrees of freedom. For example, in a two-sample T-test, the P-value can be found using a T-distribution table or calculator, given the T-statistic and the degrees of freedom.
• 2. Analysis of Variance (ANOVA): ANOVA is used to compare means among three or more groups. The P-value in ANOVA is calculated based on the F-statistic, which compares the variance between groups to the variance within groups. A small P-value indicates that at least one group mean is significantly different from the others.
• 3. Chi-Square Test: For categorical data, the Chi-Square test is used to determine if there is a significant association between two variables. The P-value is calculated based on the Chi-Square statistic and the degrees of freedom, indicating whether the observed frequencies significantly differ from the expected frequencies under the null hypothesis of no association.
• 4. Non-Parametric Tests: For data that do not meet the assumptions of parametric tests (e.g., normality), non-parametric tests such as the Wilcoxon rank-sum test (for comparing two groups) or the Kruskal-Wallis test (for comparing more than two groups) can be used. These tests calculate the P-value based on the ranks of the data rather than the actual values.
• 5. Bootstrap Sampling: This method involves resampling the data with replacement many times, calculating the test statistic for each resample, and then determining the proportion of times the test statistic is at least as extreme as the one observed in the original sample. This proportion serves as an estimate of the P-value.

Interpreting P-Values

Interpreting P-values correctly is crucial. A P-value less than the chosen alpha level (commonly 0.05) leads to the rejection of the null hypothesis, suggesting that the observed effect is statistically significant. However, it’s essential to remember that statistical significance does not necessarily imply practical significance. The effect size and the context of the study should also be considered when interpreting the results.

Common Misinterpretations

There are several common misinterpretations of P-values: - Misunderstanding the null hypothesis: The null hypothesis is often misunderstood as the hypothesis of no effect, but it specifically states that there is no effect or difference of a particular type. - Confusing statistical significance with practical significance: Just because a result is statistically significant, it does not mean it has practical importance. - Believing that the P-value measures the probability that the null hypothesis is true: The P-value does not tell us the probability that the null hypothesis is true; it tells us the probability of observing our data (or more extreme) if the null hypothesis is true.

Test	Description	P-Value Interpretation
Z-Test/T-Test	Compare mean of sample to population mean or compare means of two samples	P-value indicates probability of observing the test statistic under the null hypothesis
ANOVA	Compare means among three or more groups	P-value indicates whether at least one group mean is significantly different
Chi-Square Test	Determine association between two categorical variables	P-value indicates whether observed frequencies significantly differ from expected frequencies

📝 Note: The choice of statistical test depends on the research question, the type of data, and the assumptions met by the data.

In summary, determining the P-value is a critical step in hypothesis testing, providing insight into whether the observed effects are due to chance or if they reflect real differences or relationships. By understanding and correctly interpreting P-values, researchers can draw more accurate conclusions from their data.