5 Ways To Calculate Z-Score
Introduction to Z-Score Calculation
The Z-score, also known as the standard score, is a statistical measure that describes a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean. If a value has a Z-score of 0, it is equal to the mean. A Z-score of 1 means the value is 1 standard deviation from the mean, and so on. Calculating the Z-score is essential in various statistical analyses, including hypothesis testing and confidence intervals. In this article, we will explore five ways to calculate the Z-score, each applicable to different scenarios or data types.
Understanding the Z-Score Formula
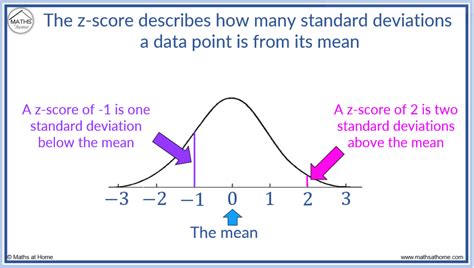
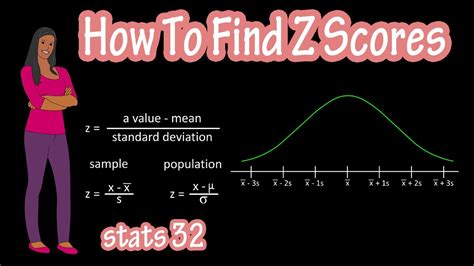
Before diving into the different methods, it’s crucial to understand the basic Z-score formula: [ Z = \frac{(X - \mu)}{\sigma} ] where: - ( Z ) is the Z-score, - ( X ) is the value of the element, - ( \mu ) is the mean of the dataset, - ( \sigma ) is the standard deviation of the dataset. This formula is the foundation for calculating Z-scores, and variations of it will be used in the methods described below.
Method 1: Calculating Z-Score for a Single Data Point

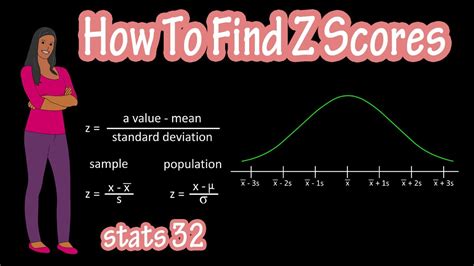
To calculate the Z-score for a single data point, you need to know the mean (( \mu )) and standard deviation (( \sigma )) of the dataset. Here are the steps: - Step 1: Find the mean (( \mu )) of your dataset. - Step 2: Calculate the standard deviation (( \sigma )) of your dataset. - Step 3: Subtract the mean from your data point (( X - \mu )). - Step 4: Divide the result by the standard deviation. For example, if ( X = 25 ), ( \mu = 20 ), and ( \sigma = 5 ), then: [ Z = \frac{(25 - 20)}{5} = \frac{5}{5} = 1 ] This means the data point is 1 standard deviation above the mean.
Method 2: Using Z-Score Tables or Z-Tables
Another way to find Z-scores is by using Z-score tables, also known as Z-tables. These tables provide the area to the left of a given Z-score in a standard normal distribution. To use a Z-table: - Step 1: Calculate the Z-score using the formula ( Z = \frac{(X - \mu)}{\sigma} ). - Step 2: Look up the Z-score in the Z-table to find the corresponding probability or area under the curve. For instance, if you calculate a Z-score of 1.5, you can look up 1.5 in the Z-table to find the area to the left of this Z-score.
Method 3: Calculating Z-Score for a Sample

When working with a sample of data, you might not know the population mean (( \mu )) or standard deviation (( \sigma )). In such cases, you can use the sample mean (( \bar{X} )) and sample standard deviation (( s )) as estimates. The formula slightly adjusts to: [ Z = \frac{(X - \bar{X})}{s} ] However, when calculating the Z-score for a new value based on a sample, it’s essential to use the sample standard deviation and consider the degrees of freedom for more accurate results, especially in small samples.
Method 4: Using Technology and Software
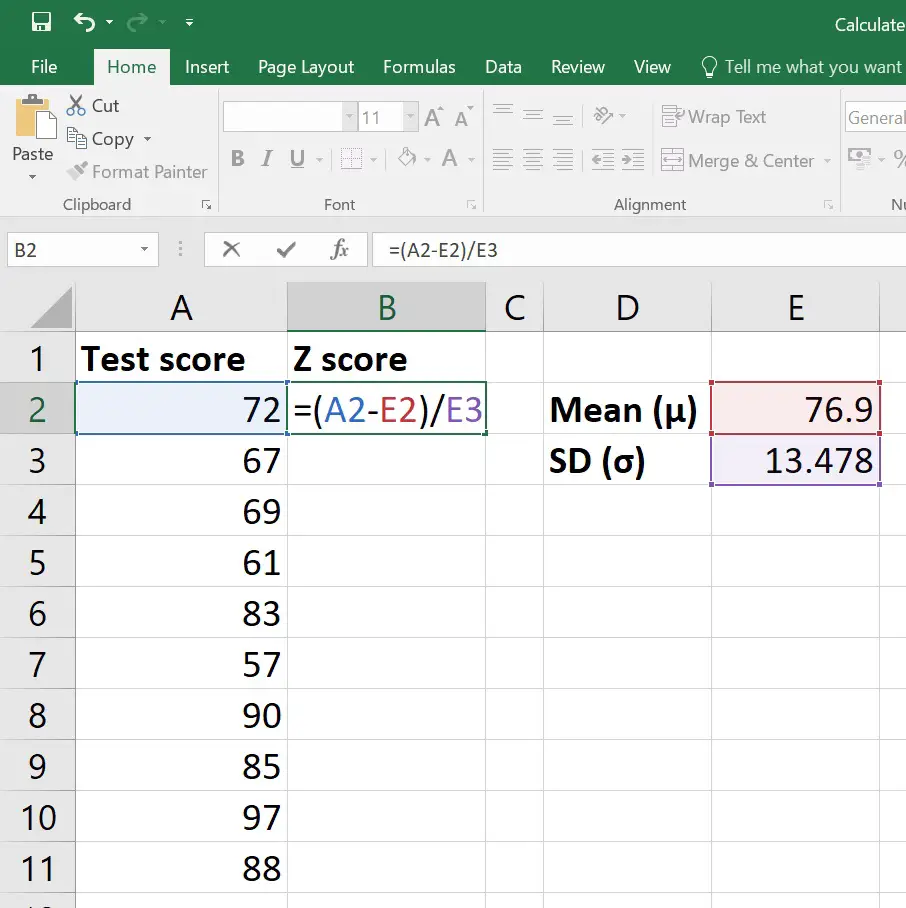
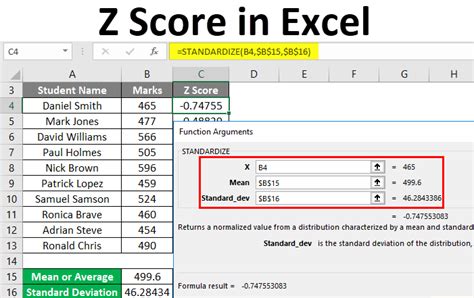
With the advancement of technology, calculating Z-scores can be simplified using statistical software or calculators. Programs like Excel, R, Python (with libraries such as Pandas and NumPy), and statistical calculators can compute Z-scores directly. For example: - In Excel, you can use the
STANDARDIZE function to calculate Z-scores.
- In Python, libraries like SciPy provide functions to calculate Z-scores.
These tools can save time and reduce errors in calculation, especially when dealing with large datasets.
Method 5: Online Z-Score Calculators

For quick calculations or when you don’t have access to statistical software, online Z-score calculators can be very useful. These tools usually require you to input the value, mean, and standard deviation, and then they calculate the Z-score for you. This method is straightforward and requires minimal mathematical knowledge, making it accessible to a wide range of users.
📝 Note: When using online calculators or software, ensure you understand the input requirements and the assumptions made by the calculator, as different tools might use slightly different formulas based on the context (population vs. sample).
Applications of Z-Score Calculation
Z-scores have numerous applications in statistics and data analysis, including: - Hypothesis Testing: Z-scores are used to determine how many standard deviations an element is from the mean, which is crucial in hypothesis testing. - Confidence Intervals: Z-scores help in constructing confidence intervals for population means. - Comparing Data Points: Z-scores allow for the comparison of data points from different datasets by standardizing them.
Importance of Z-Score in Data Analysis

The Z-score is a powerful tool in data analysis because it allows for the comparison of data points on a common scale. This is particularly useful when dealing with datasets that have different units or scales. By converting data points into Z-scores, analysts can: - Identify Outliers: Data points with high absolute Z-scores (typically greater than 2 or less than -2) are considered outliers. - Standardize Data: Z-scores are used to standardize data, which is essential for many statistical analyses and machine learning algorithms. - Compare Distributions: Z-scores enable the comparison of data points from different distributions, facilitating a deeper understanding of the data.
What is the main use of Z-scores in statistics?

+
Z-scores are primarily used to understand how many standard deviations an element is from the mean. This is crucial in hypothesis testing, constructing confidence intervals, and comparing data points from different datasets.
Can Z-scores be used for non-normal distributions?
+
While Z-scores are typically used with normal distributions, there are methods to apply similar concepts to non-normal distributions, such as using transformations to normalize the data or employing non-parametric tests. However, the interpretation and applicability might differ.
How do I choose the right method for calculating Z-scores?

+
The choice of method depends on the nature of your data (sample vs. population), the tools available to you (software, calculators, online tools), and your specific analytical needs (hypothesis testing, confidence intervals, etc.). Understanding the assumptions and limitations of each method is key to making an informed decision.
In summary, calculating Z-scores is a fundamental aspect of statistical analysis, allowing for the standardization of data points and facilitating comparisons across different datasets. The various methods for calculating Z-scores, from manual calculations to the use of software and online tools, provide flexibility and accessibility for analysts. By understanding and applying these methods appropriately, data analysts can leverage Z-scores to uncover valuable insights within their data.