5 Ways Calculate Uncertainty
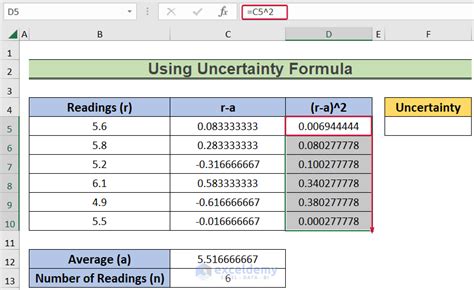
Introduction to Uncertainty Calculation

Calculating uncertainty is a crucial step in various fields, including science, engineering, and finance. It helps in understanding the reliability of measurements, predictions, and outcomes. There are several methods to calculate uncertainty, each with its own strengths and applications. In this article, we will explore five ways to calculate uncertainty, highlighting their principles, advantages, and typical use cases.
1. Standard Deviation Method

The standard deviation method is one of the most commonly used techniques for calculating uncertainty. It measures the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation is calculated as the square root of the variance, which is the average of the squared differences from the mean.
2. Margin of Error Method
The margin of error method is often used in statistical analysis and survey research. It estimates the maximum amount by which the sample results may differ from the true population values. The margin of error is calculated based on the sample size, confidence level, and standard deviation of the sample. This method provides a range within which the true value is likely to lie, giving an indication of the uncertainty associated with the estimate.
3. Confidence Interval Method
The confidence interval method provides a range of values within which a population parameter is likely to lie. It is constructed from a sample of data and is used to estimate the population mean or proportion. A confidence interval gives an indication of the uncertainty associated with the estimate, with a wider interval indicating greater uncertainty. The confidence level, usually expressed as a percentage (e.g., 95%), reflects the probability that the interval contains the true population parameter.
4. Monte Carlo Simulation Method

The Monte Carlo simulation method is a computational technique used to estimate the uncertainty associated with complex systems or processes. It involves generating multiple scenarios or simulations, each with random variations in input parameters, to predict the range of possible outcomes. This method is particularly useful in situations where the relationships between variables are complex or nonlinear, making it difficult to apply traditional statistical methods.
5. Bayesian Method
The Bayesian method is a statistical approach that updates the probability of a hypothesis based on new data or evidence. It can be used to quantify uncertainty by estimating the probability distribution of a parameter or outcome. Bayesian inference involves updating the prior distribution with the likelihood of observing the data, given the hypothesis, to obtain the posterior distribution. This method provides a flexible framework for incorporating expert judgment and prior knowledge into the analysis of uncertainty.
💡 Note: The choice of method depends on the nature of the problem, the type of data available, and the level of complexity involved. Each method has its strengths and limitations, and the selection of the most appropriate technique requires careful consideration of these factors.
In practice, calculating uncertainty involves several steps, including: * Identifying the sources of uncertainty * Quantifying the uncertainty using one or more of the methods described above * Interpreting the results in the context of the problem or decision at hand * Communicating the uncertainty to stakeholders or decision-makers
| Method | Description | Advantages | Disadvantages |
|---|---|---|---|
| Standard Deviation | Measures variation in a dataset | Easy to calculate, widely applicable | Assumes normal distribution, sensitive to outliers |
| Margin of Error | Estimates the maximum error in a sample estimate | Provides a clear indication of uncertainty, widely used in surveys | Assumes random sampling, may not account for non-sampling errors |
| Confidence Interval | Provides a range of values for a population parameter | Gives a clear indication of uncertainty, widely applicable | Assumes normal distribution, may be wide or narrow depending on sample size |
| Monte Carlo Simulation | Estimates uncertainty through computational simulations | Flexible, can handle complex systems or processes | Computationally intensive, requires expertise in simulation methods |
| Bayesian Method | Updates the probability of a hypothesis based on new data | Flexible, can incorporate prior knowledge or expert judgment | Requires expertise in Bayesian inference, can be computationally intensive |
As we reflect on the different methods for calculating uncertainty, it becomes clear that each approach has its unique strengths and limitations. By understanding these methods and their applications, we can better navigate the complexities of uncertainty and make more informed decisions in a wide range of fields. Whether in science, engineering, finance, or other areas, the ability to quantify and communicate uncertainty is essential for advancing knowledge, managing risk, and driving innovation.
What is the most commonly used method for calculating uncertainty?
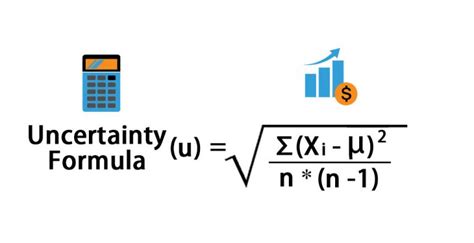
+
The standard deviation method is one of the most commonly used techniques for calculating uncertainty, as it provides a clear indication of the variation or dispersion in a dataset.
How do I choose the right method for calculating uncertainty?

+
The choice of method depends on the nature of the problem, the type of data available, and the level of complexity involved. Consider the strengths and limitations of each method, as well as the expertise and resources required for implementation.
Can I use multiple methods for calculating uncertainty?
+
Yes, it is possible to use multiple methods for calculating uncertainty, depending on the specific requirements of the problem or decision at hand. Combining methods can provide a more comprehensive understanding of uncertainty and its implications.