Factorial ANOVA Setup in Excel
Introduction to Factorial ANOVA
When dealing with experimental designs that involve more than one independent variable, factorial ANOVA becomes a crucial statistical tool. It helps in understanding the interaction effects between these variables on the dependent variable. In this context, setting up a factorial ANOVA in Excel is a practical approach to analyze such complex data sets. Excel, with its powerful analysis tools, including the Analysis ToolPak, facilitates this process.
Understanding Factorial ANOVA
Before diving into the setup process, it’s essential to grasp the basics of factorial ANOVA. Factorial ANOVA is used in experiments where there are two or more independent variables (factors) to determine if there is an interaction between them that affects the dependent variable. Each factor can have multiple levels, and the analysis looks at main effects (the effect of each factor individually) and interaction effects (how the factors affect each other).
Setting Up Factorial ANOVA in Excel

To set up a factorial ANOVA in Excel, follow these steps:
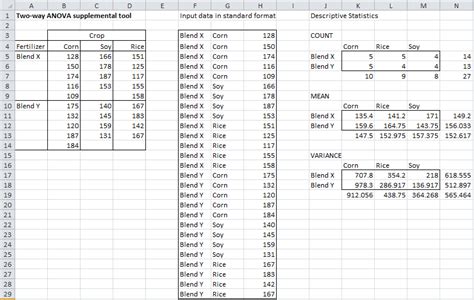
Prepare Your Data: Ensure your data is organized in a way that each row represents a single observation, and columns represent variables. For a factorial ANOVA, you’ll have at least three columns: one for the dependent variable and at least two for the independent variables (factors).
Install Analysis ToolPak: If you haven’t already, you’ll need to install the Analysis ToolPak in Excel. This add-in provides the statistical tools necessary for ANOVA analysis. To install it, go to File > Options > Add-ins, and then check Analysis ToolPak and click OK.
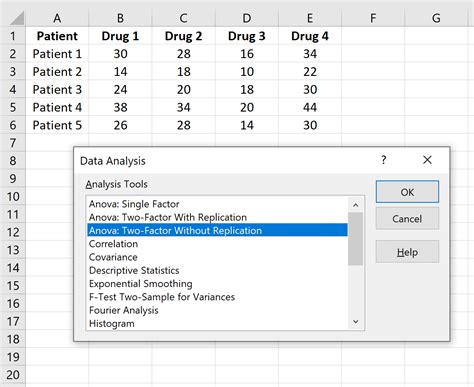
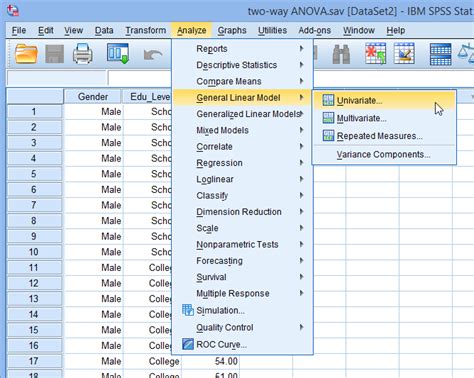
Access ANOVA Tool: With your data ready and the Analysis ToolPak installed, go to the Data tab, click on Data Analysis in the Analysis group, and then select Anova: Two-Factor With Replication or Anova: Single Factor depending on your data structure. For factorial ANOVA involving more than two factors, you might need to use Anova: Two-Factor With Replication and adjust your data accordingly or use more advanced statistical software for higher-order ANOVA.
Input Your Data: In the dialog box that appears, input the range of your data. Ensure you select the entire range including headers if you want them included in the output. Also, specify the number of levels in each factor if prompted.
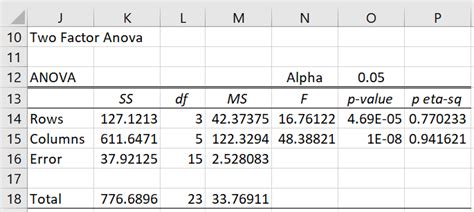
Run the Analysis: Click OK to run the ANOVA analysis. Excel will then produce an output table that includes the results of your analysis, such as the F-statistic, p-value, and degrees of freedom for each main effect and interaction effect.
Interpreting the Results
- F-statistic and p-value: A low p-value (typically less than 0.05) indicates that the effect of the factor (or interaction) on the dependent variable is statistically significant. - Degrees of Freedom: Used in calculating the F-statistic, understanding degrees of freedom helps in interpreting the F-distribution and thus the significance of the results.
Example Scenario
Consider an experiment where you’re testing the effect of temperature (high, medium, low) and pH level (acidic, basic) on the yield of a chemical reaction. Your data might look something like this:
| Temperature | pH Level | Yield |
|---|---|---|
| High | Acidic | 10 |
| High | Basic | 12 |
| Medium | Acidic | 8 |
| Medium | Basic | 11 |
| Low | Acidic | 7 |
| Low | Basic | 9 |
By applying factorial ANOVA to this data, you could determine if temperature, pH level, or the interaction between them significantly affects the yield of the chemical reaction.
📝 Note: Always ensure your data meets the assumptions of ANOVA, such as normality of residuals and homogeneity of variances, before drawing conclusions from your analysis.
In summary, setting up a factorial ANOVA in Excel is a straightforward process once you have your data organized and the necessary tools installed. It provides a powerful method for analyzing the effects of multiple independent variables on a dependent variable, including interactions between these variables.
What is the main purpose of using factorial ANOVA in data analysis?
+
The main purpose of using factorial ANOVA is to understand the effects of two or more independent variables on a dependent variable, including the interaction effects between these variables.
How do I interpret the results of a factorial ANOVA analysis?
+
Interpretation involves looking at the p-value for each main effect and interaction to determine statistical significance. A p-value less than 0.05 typically indicates significance.
What are the assumptions of ANOVA that need to be met before analysis?

+
Key assumptions include the normality of residuals, homogeneity of variances, and independence of observations. Violations of these assumptions may require alternative analyses or data transformations.