5 Ways Calculate Percentage

Introduction to Calculating Percentages

Calculating percentages is a fundamental mathematical skill that is used in various aspects of life, including finance, statistics, and everyday applications. A percentage is a way to express a value as a fraction of 100. It is often denoted by the symbol “%”. In this article, we will explore five ways to calculate percentages, making it easier for you to understand and apply this concept in different scenarios.

Method 1: Finding a Percentage of a Number

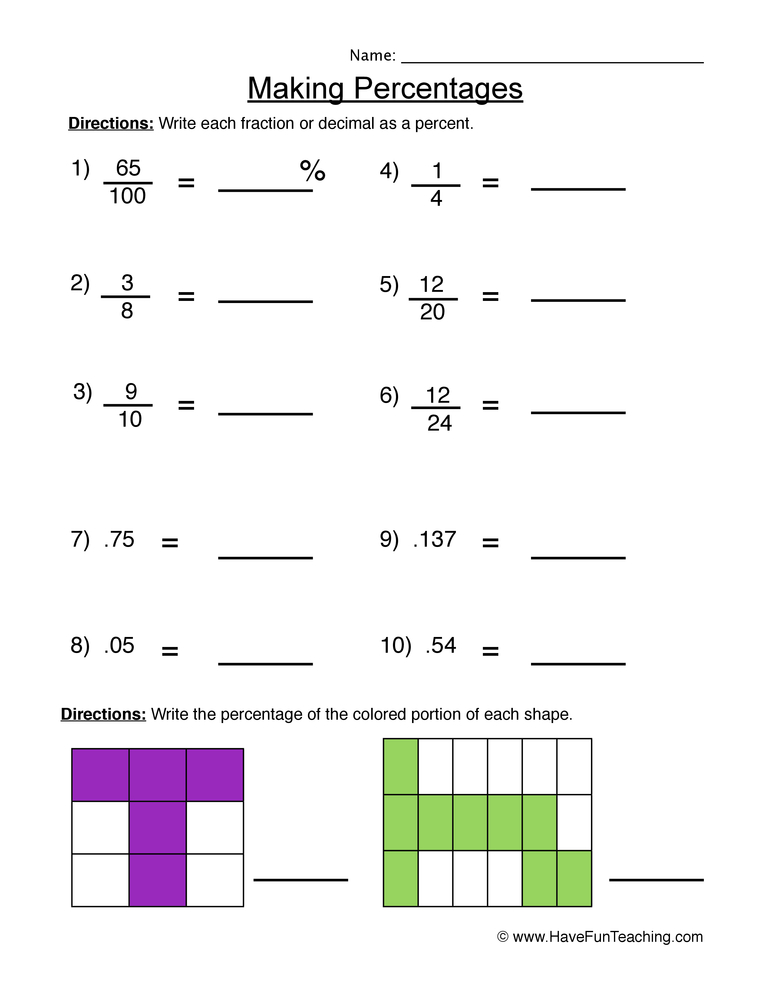
To find a percentage of a number, you can use the formula: [ \text{Percentage of a number} = \left( \frac{\text{percentage}}{100} \right) \times \text{number} ] For example, if you want to find 25% of 200, you would calculate it as follows: [ 25\% \text{ of } 200 = \left( \frac{25}{100} \right) \times 200 = 0.25 \times 200 = 50 ] This means 25% of 200 is 50.

Method 2: Calculating the Percentage Increase

The percentage increase can be calculated using the formula: [ \text{Percentage increase} = \left( \frac{\text{increase}}{\text{original value}} \right) \times 100 ] For instance, if the price of a product increases from 100 to 120, the percentage increase can be calculated as: [ \text{Percentage increase} = \left( \frac{120 - 100}{100} \right) \times 100 = \left( \frac{20}{100} \right) \times 100 = 20\% ] This indicates a 20% increase in price.

Method 3: Calculating the Percentage Decrease

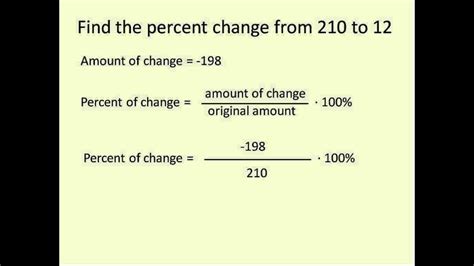
Similarly, to calculate the percentage decrease, you use the formula: [ \text{Percentage decrease} = \left( \frac{\text{decrease}}{\text{original value}} \right) \times 100 ] If the price of a product decreases from 100 to 80, the percentage decrease can be calculated as: [ \text{Percentage decrease} = \left( \frac{100 - 80}{100} \right) \times 100 = \left( \frac{20}{100} \right) \times 100 = 20\% ] This shows a 20% decrease in price.

Method 4: Finding the Original Value Before a Percentage Change

If you know the final value after a percentage change and want to find the original value, you can rearrange the formula to solve for the original value. For a percentage increase: [ \text{Original value} = \frac{\text{final value}}{1 + \left( \frac{\text{percentage increase}}{100} \right)} ] For a percentage decrease: [ \text{Original value} = \frac{\text{final value}}{1 - \left( \frac{\text{percentage decrease}}{100} \right)} ] For example, if a product is on sale for 120 after a 20% increase, the original price can be found as: \[ \text{Original value} = \frac{120}{1 + \left( \frac{20}{100} \right)} = \frac{120}{1.2} = 100 \] This means the original price was 100.

Method 5: Comparing Percentages

When comparing percentages, it’s essential to understand that the base value can affect the outcome significantly. For instance, a 10% increase on a small base value might result in a smaller absolute change compared to the same percentage increase on a larger base value. To compare percentages effectively, consider both the percentage change and the base value it’s applied to.

Scenario	Base Value	Percentage Change	Absolute Change
Small Base	100</td> <td>10%</td> <td>10
Large Base	1000</td> <td>10%</td> <td>100

In this example, although the percentage increase is the same (10%), the absolute change differs significantly due to the difference in base values.

📝 Note: When dealing with percentages, it's crucial to understand the context, including the base value and the type of percentage change (increase or decrease), to make accurate calculations and comparisons.

As we’ve explored various methods for calculating percentages, it’s clear that understanding percentages is vital for making informed decisions in personal finance, business, and other areas. By applying these methods, you can better analyze data, compare changes, and predict future trends based on percentage changes.

To recap, calculating percentages involves understanding the concept of a percentage as a fraction of 100 and applying it to different scenarios, such as finding a percentage of a number, calculating percentage increases and decreases, finding original values before percentage changes, and comparing percentages across different base values. Each method provides a unique insight into how percentages can be used to analyze and interpret data, making them a powerful tool in both everyday applications and professional settings.