5 Ways To Rotate

Introduction to Rotation

Rotation is a fundamental concept in various fields, including mathematics, physics, engineering, and computer science. It refers to the act of turning an object around a fixed point, known as the axis of rotation. Rotation can be performed in different ways, and understanding these methods is essential for solving problems and manipulating objects in various contexts. In this article, we will explore five ways to rotate objects, including 2D rotation, 3D rotation, matrix rotation, quaternion rotation, and axis-angle rotation.

2D Rotation

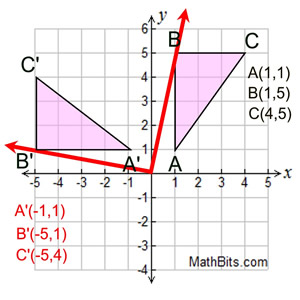
2D rotation involves rotating an object in a two-dimensional space. This can be achieved using the following formula: x’ = x * cos(θ) - y * sin(θ) y’ = x * sin(θ) + y * cos(θ) where (x, y) are the original coordinates, (x’, y’) are the rotated coordinates, and θ is the angle of rotation. This method is commonly used in computer graphics, game development, and engineering.

3D Rotation

3D rotation involves rotating an object in a three-dimensional space. This can be achieved using the following formulas: x’ = x * cos(θ) - y * sin(θ) y’ = x * sin(θ) + y * cos(θ) z’ = z where (x, y, z) are the original coordinates, (x’, y’, z’) are the rotated coordinates, and θ is the angle of rotation. However, in 3D space, we need to consider the axis of rotation, which can be any of the three axes (x, y, or z). This method is commonly used in computer-aided design (CAD), computer-generated imagery (CGI), and robotics.

Matrix Rotation

Matrix rotation involves using matrices to perform rotations. A rotation matrix is a square matrix that, when multiplied by a vector, rotates the vector by a certain angle. The rotation matrix for 2D rotation is:

cos(θ)	-sin(θ)
sin(θ)	cos(θ)

where θ is the angle of rotation. This method is commonly used in linear algebra, computer graphics, and game development.

Quaternion Rotation

Quaternion rotation involves using quaternions to perform rotations. A quaternion is a mathematical object that can be used to represent 3D rotations. The quaternion rotation formula is: q’ = q * q_rot where q is the original quaternion, q_rot is the rotation quaternion, and q’ is the rotated quaternion. This method is commonly used in computer graphics, game development, and robotics.

Axis-Angle Rotation

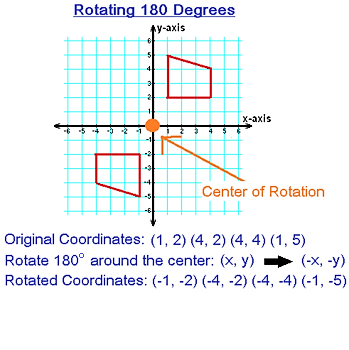
Axis-angle rotation involves rotating an object around a fixed axis by a certain angle. The axis-angle rotation formula is: v’ = v * cos(θ) + (k × v) * sin(θ) + k * (k · v) * (1 - cos(θ)) where v is the original vector, v’ is the rotated vector, k is the axis of rotation, and θ is the angle of rotation. This method is commonly used in computer graphics, game development, and engineering.

📝 Note: Understanding the different rotation methods is crucial for solving problems and manipulating objects in various contexts.

In summary, there are various ways to rotate objects, including 2D rotation, 3D rotation, matrix rotation, quaternion rotation, and axis-angle rotation. Each method has its own strengths and weaknesses, and the choice of method depends on the specific application and context. By understanding these methods, we can better manipulate objects and solve problems in various fields.