5 Ways Calculate Rate

Introduction to Calculating Rates

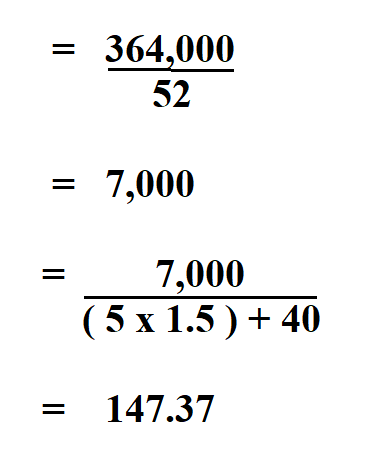
Calculating rates is a fundamental concept in various fields, including mathematics, physics, economics, and finance. A rate is a measure of the change in one quantity with respect to another quantity. It is often expressed as a ratio of two quantities, where one quantity is the change in the other quantity over a specific period or distance. In this article, we will explore five ways to calculate rates, providing a comprehensive understanding of the concept and its applications.

1. Calculating Rate as a Ratio

The most basic way to calculate a rate is by expressing it as a ratio of two quantities. This is often represented mathematically as rate = change in quantity / change in time or rate = distance / time. For instance, if an object travels 200 miles in 4 hours, its speed (rate of distance over time) can be calculated as 200 miles / 4 hours = 50 miles per hour. This method is widely used in physics and engineering to calculate velocities, accelerations, and other rates of change.

2. Using the Formula: Rate = (End Value - Start Value) / Time

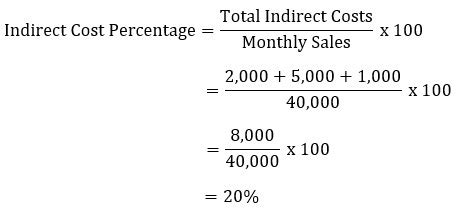
Another common method for calculating rates involves using the formula: rate = (end value - start value) / time. This formula is particularly useful in finance and economics, where it is used to calculate rates of return on investments, inflation rates, and interest rates. For example, if an investment grows from 1000 to 1200 over 2 years, the rate of return can be calculated as (1200 - 1000) / 2 years = 200 / 2 years = 100 per year.

3. Calculating Rate Using Proportional Relationships

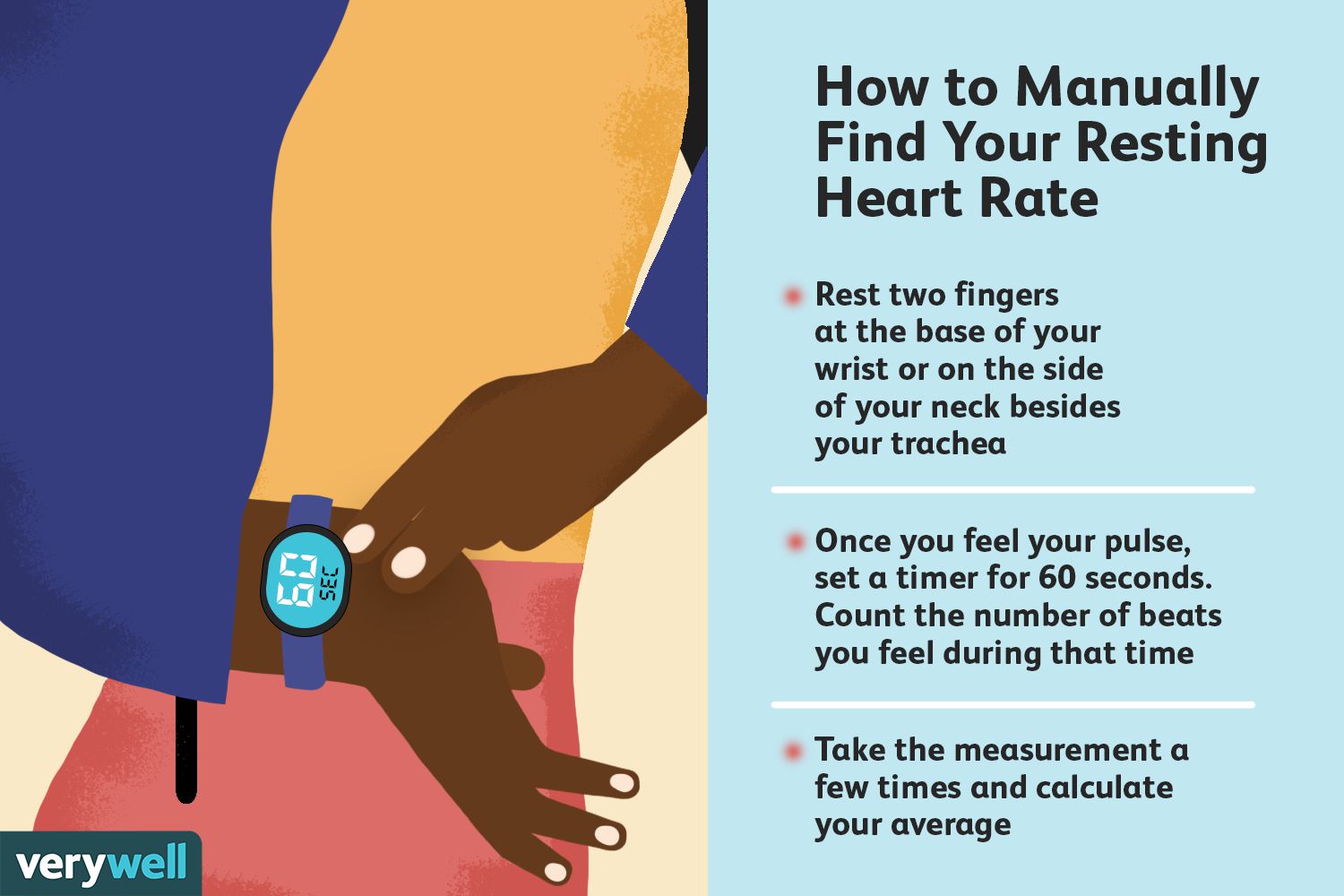
Rates can also be calculated by recognizing proportional relationships between quantities. If two quantities are directly proportional, their ratio is constant. For instance, the distance traveled by an object moving at a constant speed is directly proportional to the time it travels. By recognizing these proportional relationships, rates can be calculated even when some information is missing. For example, if it is known that 3 meters of wire is used for every 5 units of a product, and 12 meters of wire are used, the number of product units can be calculated using the proportional relationship, thereby allowing for the calculation of a rate related to production efficiency.

4. Using Slope to Calculate Rate of Change

In graphing and calculus, the slope of a line or curve represents the rate of change of one variable with respect to another. For linear relationships, the slope (m) can be calculated using the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line. This slope represents the rate of change of y with respect to x. For more complex relationships, derivatives are used to find the rate of change at any point. This method is crucial in understanding how quantities change in response to each other, with applications in physics, economics, and optimization problems.

5. Calculating Rate Using Average and Instantaneous Rates

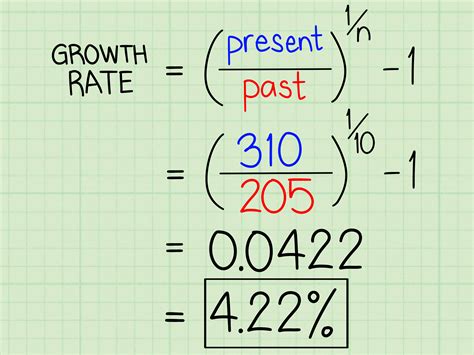
Finally, rates can be calculated by distinguishing between average and instantaneous rates. The average rate of change is calculated over a specified interval and provides a general measure of how one quantity changes with respect to another over that interval. In contrast, the instantaneous rate of change, found using derivatives in calculus, gives the rate of change at a specific point in time. Understanding the difference between these two types of rates is essential in many applications, from calculating the average speed of a vehicle over a trip to determining the instantaneous velocity at any given moment.

📝 Note: Calculating rates accurately is crucial for making informed decisions and predictions in various fields. Understanding the different methods for calculating rates enhances problem-solving capabilities and analytical thinking.

To summarize the key points, calculating rates involves expressing change as a ratio, using formulas to find rates of change over time, recognizing proportional relationships, interpreting slopes as rates of change, and distinguishing between average and instantaneous rates. Each of these methods has its applications and importance in different fields, making the concept of rate calculation versatile and fundamental.