5 Ways Add Exponents
Understanding Exponents

Exponents are a fundamental concept in mathematics, used to represent repeated multiplication of a number by itself. For instance, 2^3 means 2 multiplied by itself 3 times, which equals 2 * 2 * 2 = 8. Mastering exponents is crucial for various mathematical operations and solving equations. In this article, we will explore five ways to add exponents, ensuring a comprehensive understanding of the subject.
Method 1: Adding Exponents with the Same Base

When adding exponents with the same base, we can use the rule a^m + a^n = a^m + a^n, but only if the exponents are the same can we combine them using the formula a^m * a^n = a^(m+n). However, this rule does not apply when adding two different powers of the same base. For example, 2^3 + 2^4 cannot be directly combined using this rule. Instead, we calculate each term separately: 2^3 = 8 and 2^4 = 16, then add them together to get 8 + 16 = 24.
Method 2: Using the Distributive Property
The distributive property allows us to distribute a single term across the terms inside the parentheses. This property can be useful when dealing with expressions that involve adding exponents. For example, if we have 2 * (3^2 + 4^2), we can use the distributive property to expand it: 2 * 3^2 + 2 * 4^2. Then, calculate each term separately: 2 * 9 + 2 * 16 = 18 + 32 = 50.
Method 3: Adding Exponents with Different Bases
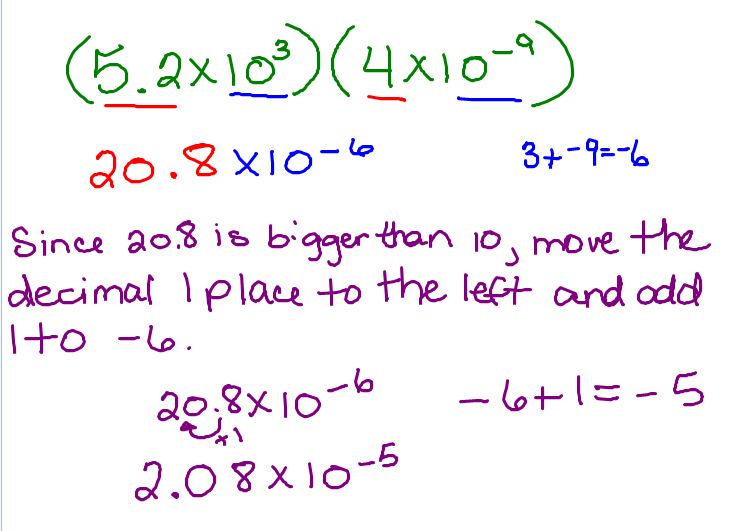
When dealing with exponents of different bases, we cannot directly add them together, even if the exponents are the same. For instance, 2^3 + 3^3 requires calculating each term separately: 2^3 = 8 and 3^3 = 27, then adding them together to get 8 + 27 = 35. There’s no rule to combine these directly because of the different bases.
Method 4: Using Algebraic Manipulation

In some cases, algebraic manipulation can help simplify expressions involving exponents. For example, consider the expression (2^2 + 3^2)^2. First, calculate the terms inside the parentheses: 2^2 = 4 and 3^2 = 9, so 4 + 9 = 13. Then, raise 13 to the power of 2: 13^2 = 169.
Method 5: Utilizing Logarithms

Logarithms can be used to simplify complex exponent expressions by turning multiplication into addition. However, this method is more advanced and typically used for equations involving very large or very small numbers. For instance, to solve 2^x = 100, we can take the logarithm of both sides to find x. This method involves understanding logarithmic properties and is useful for solving equations where exponents are unknown.
💡 Note: When working with exponents, it's essential to remember the rules of exponentiation, such as a^m * a^n = a^(m+n) and (a^m)^n = a^(m*n), to simplify and solve expressions efficiently.
In summary, adding exponents requires careful consideration of the bases and the exponents themselves. Whether using direct calculation, the distributive property, handling different bases, algebraic manipulation, or logarithms, each method has its application depending on the problem at hand. By mastering these techniques, one can efficiently solve a wide range of mathematical problems involving exponents.
What is the rule for adding exponents with the same base?

+
When the exponents are the same, you can combine them using the formula a^m * a^n = a^(m+n), but if the exponents are different, you calculate each term separately and then add them together.
How do you add exponents with different bases?

+
You calculate each term separately and then add them together. There’s no rule to directly combine exponents with different bases, even if the exponents are the same.
What is the role of logarithms in adding exponents?
+
Logarithms can be used to simplify complex exponent expressions by turning multiplication into addition, particularly useful for solving equations involving very large or very small numbers.