Hypothesis Testing in Excel

Introduction to Hypothesis Testing

Hypothesis testing is a statistical technique used to make inferences about a population based on a sample of data. It involves formulating a hypothesis, collecting data, and then using statistical methods to determine whether the hypothesis is supported or rejected. In this blog post, we will explore how to perform hypothesis testing in Excel, including the different types of tests, how to set up and interpret the results, and some common pitfalls to avoid.

Types of Hypothesis Tests

There are several types of hypothesis tests, including: * One-sample tests: Used to compare a sample mean to a known population mean. * Two-sample tests: Used to compare the means of two independent samples. * Paired tests: Used to compare the means of two related samples. * ANOVA tests: Used to compare the means of three or more independent samples.

Setting Up a Hypothesis Test in Excel

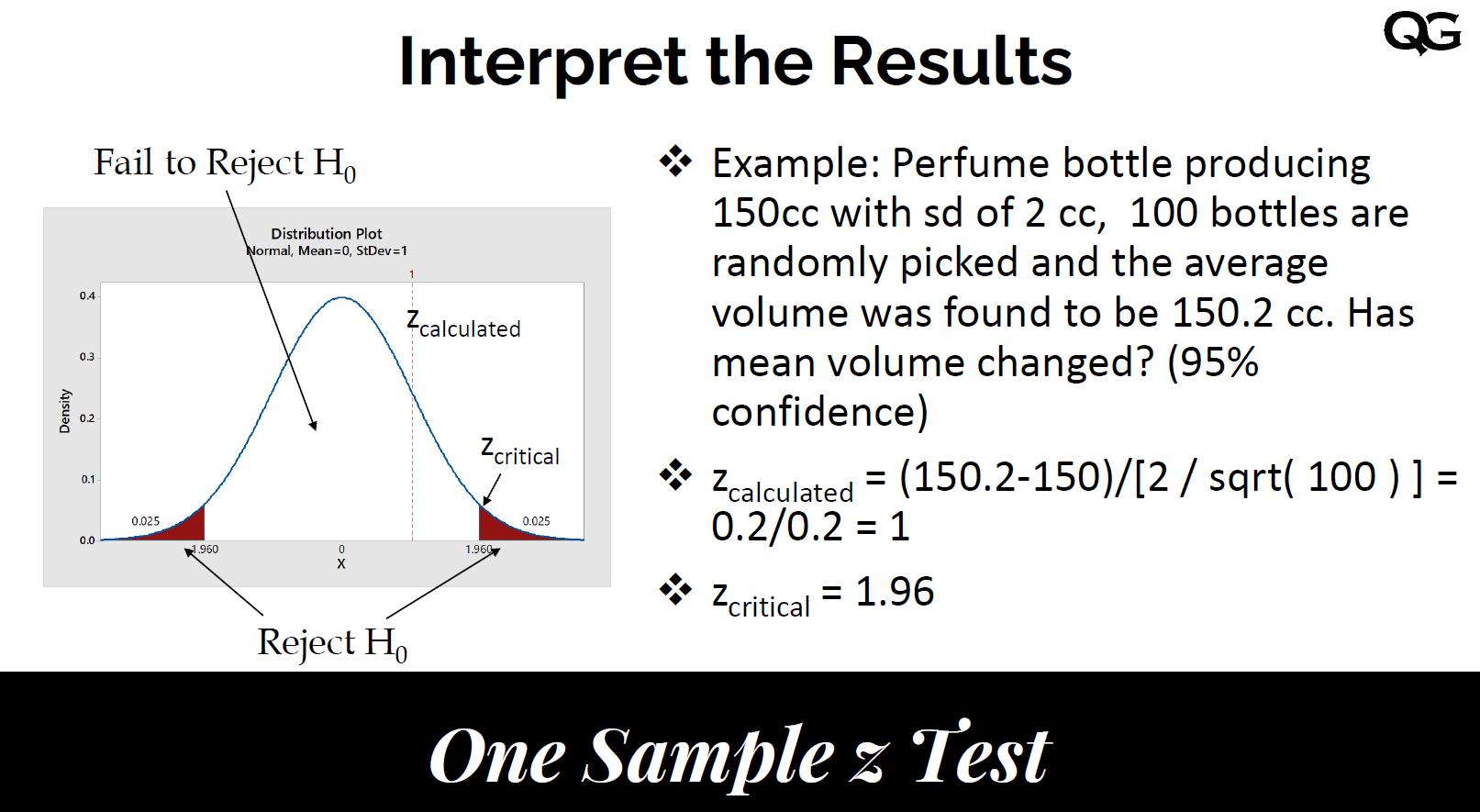
To set up a hypothesis test in Excel, you will need to: * Define the null hypothesis (H0) and the alternative hypothesis (H1). * Choose a significance level (α) for the test. * Calculate the test statistic and the p-value. * Determine whether to reject or fail to reject the null hypothesis based on the p-value.

For example, suppose we want to test whether the average height of a population of adults is greater than 175 cm. We might set up the following hypotheses: * H0: μ ≤ 175 * H1: μ > 175

We can then use Excel to calculate the test statistic and p-value, and determine whether to reject or fail to reject the null hypothesis.

Using Excel Functions for Hypothesis Testing

Excel provides several functions that can be used for hypothesis testing, including: * T.TEST: Used to perform a two-sample t-test. * T.TEST.2T: Used to perform a two-sample t-test with two-tailed test. * Z.TEST: Used to perform a one-sample z-test. * CONFIDENCE.T: Used to calculate the confidence interval for a population mean.

For example, to perform a two-sample t-test, we can use the following formula: =T.TEST(range1, range2, tails, type)

Where: * range1 is the range of values for the first sample. * range2 is the range of values for the second sample. * tails is the number of tails for the test (1 for one-tailed, 2 for two-tailed). * type is the type of test (1 for paired, 2 for unpaired).

Interpreting the Results of a Hypothesis Test

The results of a hypothesis test will typically include the test statistic, the p-value, and a decision about whether to reject or fail to reject the null hypothesis. The p-value represents the probability of obtaining the test statistic (or a more extreme value) assuming that the null hypothesis is true. If the p-value is less than the chosen significance level (α), we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.

For example, suppose we perform a two-sample t-test and obtain a p-value of 0.01. If we chose a significance level of 0.05, we would reject the null hypothesis, since the p-value is less than α.

Common Pitfalls to Avoid

There are several common pitfalls to avoid when performing hypothesis testing in Excel, including: * Failure to check assumptions: Many hypothesis tests assume that the data is normally distributed, or that the samples are independent. Failing to check these assumptions can lead to incorrect results. * Choosing the wrong test: There are many different types of hypothesis tests, and choosing the wrong one can lead to incorrect results. * Misinterpreting the results: The results of a hypothesis test can be misinterpreted if the null and alternative hypotheses are not clearly defined, or if the significance level is not chosen carefully.

Type of Test	Assumptions	Excel Function
One-sample t-test	Normality, independence	T.TEST
Two-sample t-test	Normality, independence, equal variances	T.TEST.2T
Paired t-test	Normality, independence, equal variances	T.TEST

📝 Note: It's essential to choose the correct Excel function for the type of hypothesis test you want to perform, and to carefully check the assumptions of the test.

As we can see, hypothesis testing in Excel can be a powerful tool for making inferences about a population based on a sample of data. By carefully choosing the correct test, checking assumptions, and interpreting the results, we can gain valuable insights into the characteristics of the population.

In the end, the key to successful hypothesis testing in Excel is to understand the different types of tests, how to set up and interpret the results, and how to avoid common pitfalls. With practice and experience, you can become proficient in using Excel to perform hypothesis testing and make informed decisions based on data.