5 Ways Graph Modified Goodman Diagram

Introduction to Graph Modified Goodman Diagram

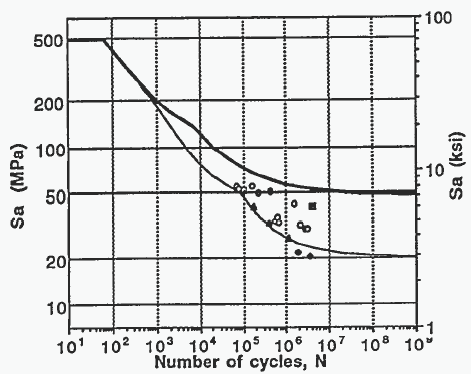
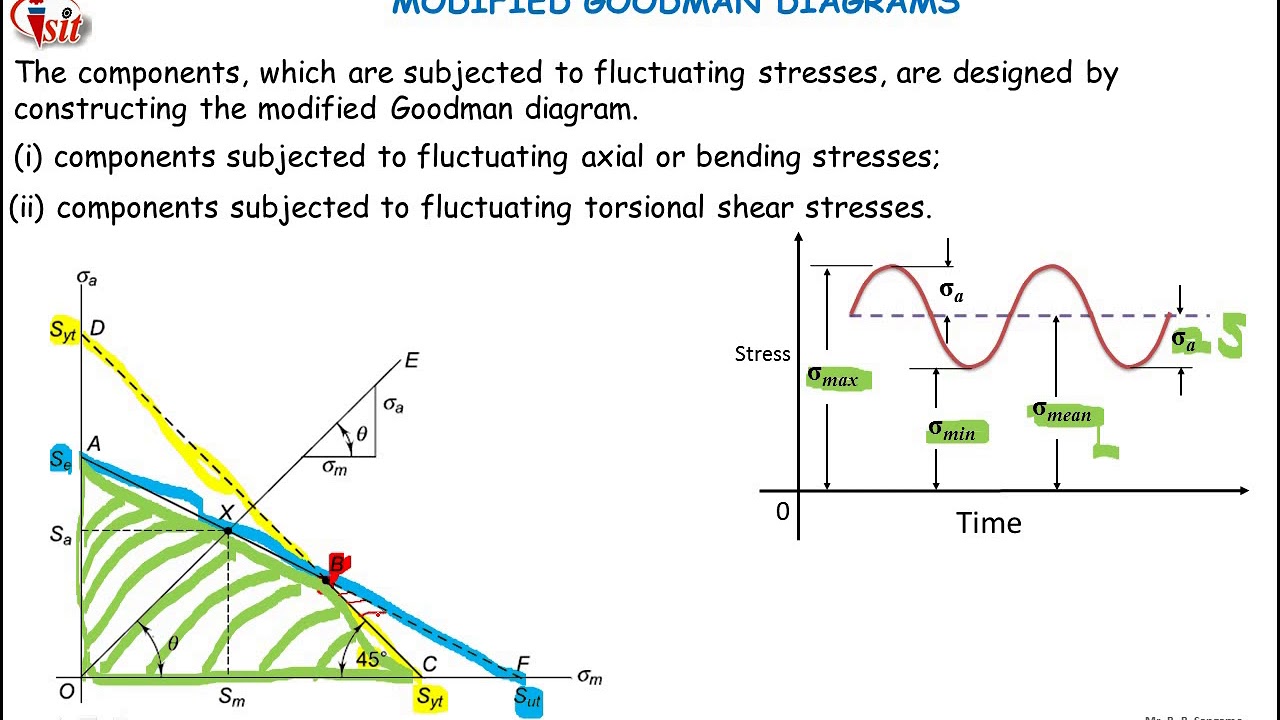
The Goodman diagram is a powerful tool used in the field of mechanics of materials to analyze the fatigue life of mechanical components under varying loads. It is particularly useful for evaluating the endurance limit of materials under alternating stresses. However, the traditional Goodman diagram has its limitations, especially when dealing with complex loading conditions or non-linear material behavior. To address these limitations, modifications to the Goodman diagram have been proposed, leading to what is known as the Graph Modified Goodman Diagram. This diagram provides a more comprehensive and accurate representation of a material’s fatigue behavior under different loading conditions.

Understanding the Goodman Diagram

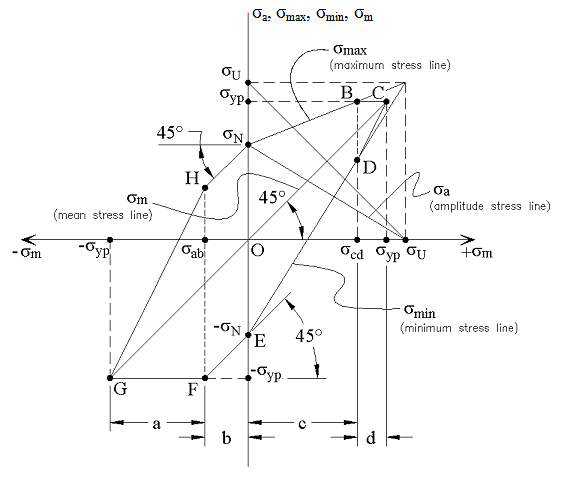
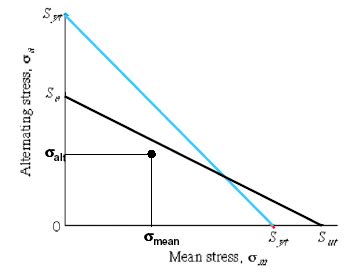
Before diving into the modifications, it’s essential to understand the basic principles of the Goodman diagram. The Goodman diagram is a graphical representation that plots the mean stress (σm) against the alternating stress (σa) to predict the endurance limit of a material. The diagram typically consists of a straight line that represents the relationship between the mean stress and the alternating stress at which failure occurs. This line is often referred to as the Goodman line. However, real-world applications often involve more complex stress states, necessitating a more nuanced approach.

Need for Modification

The traditional Goodman diagram assumes a linear relationship between the mean and alternating stresses, which may not always hold true, especially for materials exhibiting non-linear behavior or under conditions of high mean stress. Moreover, the diagram does not account for the effects of stress concentration, residual stresses, or environmental factors, which can significantly impact a component’s fatigue life. To better predict fatigue failure under these conditions, modifications to the Goodman diagram are necessary.

5 Ways Graph Modified Goodman Diagram

The Graph Modified Goodman Diagram incorporates several key modifications to improve the accuracy of fatigue life predictions. These modifications can be summarized in the following ways:

• Non-linear Relationship: The first modification involves accounting for the non-linear relationship between the mean and alternating stresses. This is achieved by using a curved line instead of a straight line to represent the failure criterion, providing a more accurate prediction of fatigue behavior under high mean stress conditions.
• Stress Concentration Factors: The second modification incorporates stress concentration factors (Kt) into the diagram. These factors account for the amplification of stresses at notches or other geometric discontinuities, allowing for a more realistic assessment of fatigue life in components with complex geometries.
• Residual Stress Effects: The third modification considers the effects of residual stresses on fatigue behavior. Residual stresses can either add to or subtract from the applied stresses, significantly affecting the endurance limit. By incorporating residual stress effects into the Goodman diagram, a more comprehensive understanding of a material’s fatigue behavior can be achieved.
• Environmental Factors: The fourth modification involves accounting for environmental factors such as temperature, humidity, and corrosive environments. These factors can drastically alter a material’s fatigue properties, and their inclusion in the modified Goodman diagram allows for more accurate predictions under real-world conditions.
• Multiaxial Stress States: The fifth modification addresses the limitation of the traditional Goodman diagram in handling multiaxial stress states. The Graph Modified Goodman Diagram can accommodate complex stress states, where principal stresses are not aligned with the material’s axes, providing a more versatile tool for analyzing fatigue under a wide range of loading conditions.

Implementation and Interpretation

Implementing these modifications into the Goodman diagram requires a thorough understanding of the material’s properties, the loading conditions, and the environmental factors at play. The interpretation of the Graph Modified Goodman Diagram involves identifying the safe region where the combination of mean and alternating stresses does not lead to fatigue failure. This safe region is bounded by the modified failure criterion line, which takes into account the non-linear relationship, stress concentration factors, residual stress effects, environmental factors, and multiaxial stress states.

💡 Note: The accuracy of the Graph Modified Goodman Diagram in predicting fatigue life depends heavily on the quality of the input data and the material's properties. Therefore, it is crucial to ensure that all parameters are accurately determined and that the diagram is applied within its limitations.

Advantages and Limitations

The Graph Modified Goodman Diagram offers several advantages over the traditional Goodman diagram, including improved accuracy under complex loading conditions, the ability to account for non-linear material behavior, and consideration of environmental factors. However, it also has limitations, such as requiring more detailed information about the material and loading conditions, and potentially being more complex to apply, especially for those without extensive experience in fatigue analysis.

Modification	Description	Advantages	Limitations
Non-linear Relationship	Accounts for non-linear behavior between mean and alternating stresses.	More accurate predictions under high mean stress conditions.	Requires accurate material property data.
Stress Concentration Factors	Incorporates effects of stress concentrations due to geometry.	Better prediction for components with complex geometries.	Requires detailed geometric analysis.
Residual Stress Effects	Considers the impact of residual stresses on fatigue behavior.	More comprehensive understanding of fatigue life.	Residual stress measurement can be challenging.
Environmental Factors	Takes into account the effects of environment on fatigue properties.	Accurate predictions under real-world conditions.	Environmental data can be difficult to obtain.
Multiaxial Stress States	Handles complex stress states not aligned with material axes.	Versatile tool for analyzing fatigue under various loading conditions.	Requires advanced understanding of stress analysis.

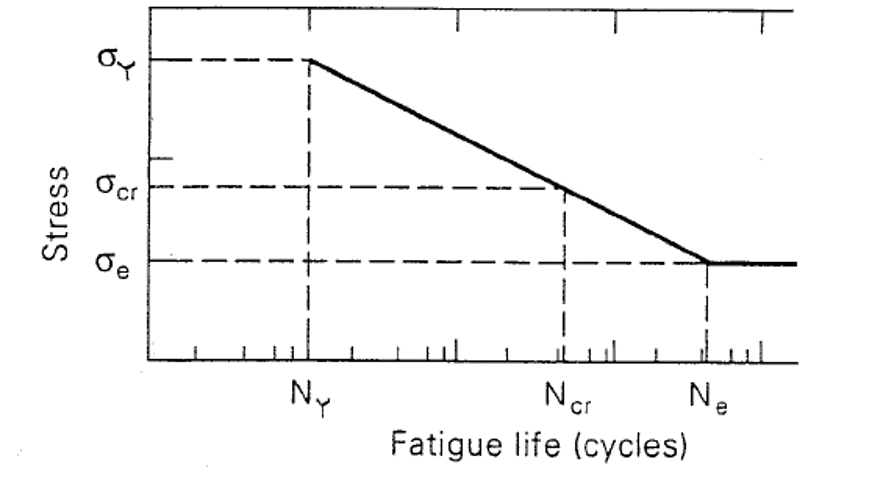
In summary, the Graph Modified Goodman Diagram is a powerful tool for predicting fatigue life under complex loading conditions. By incorporating modifications that account for non-linear material behavior, stress concentration factors, residual stress effects, environmental factors, and multiaxial stress states, it provides a more accurate and comprehensive approach to fatigue analysis compared to the traditional Goodman diagram. While it has its limitations, the advantages of the Graph Modified Goodman Diagram make it a valuable resource for engineers and researchers seeking to improve the durability and reliability of mechanical components.

To finalize, the Graph Modified Goodman Diagram represents a significant advancement in the field of fatigue analysis, offering a more nuanced and accurate method for predicting the endurance limit of materials under a wide range of loading conditions. Its application can lead to the development of more reliable and durable mechanical components, which is crucial in industries where fatigue failure can have significant consequences.