5 Ways To Get P Value
Introduction to P-Value

The p-value, or probability value, is a key concept in statistical hypothesis testing, representing the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. It is a crucial metric for determining the significance of findings in research. Calculating or obtaining the p-value can be achieved through various methods, each suited to different types of data and hypotheses. Here, we will explore five ways to get the p-value, considering the nuances and applications of each method.
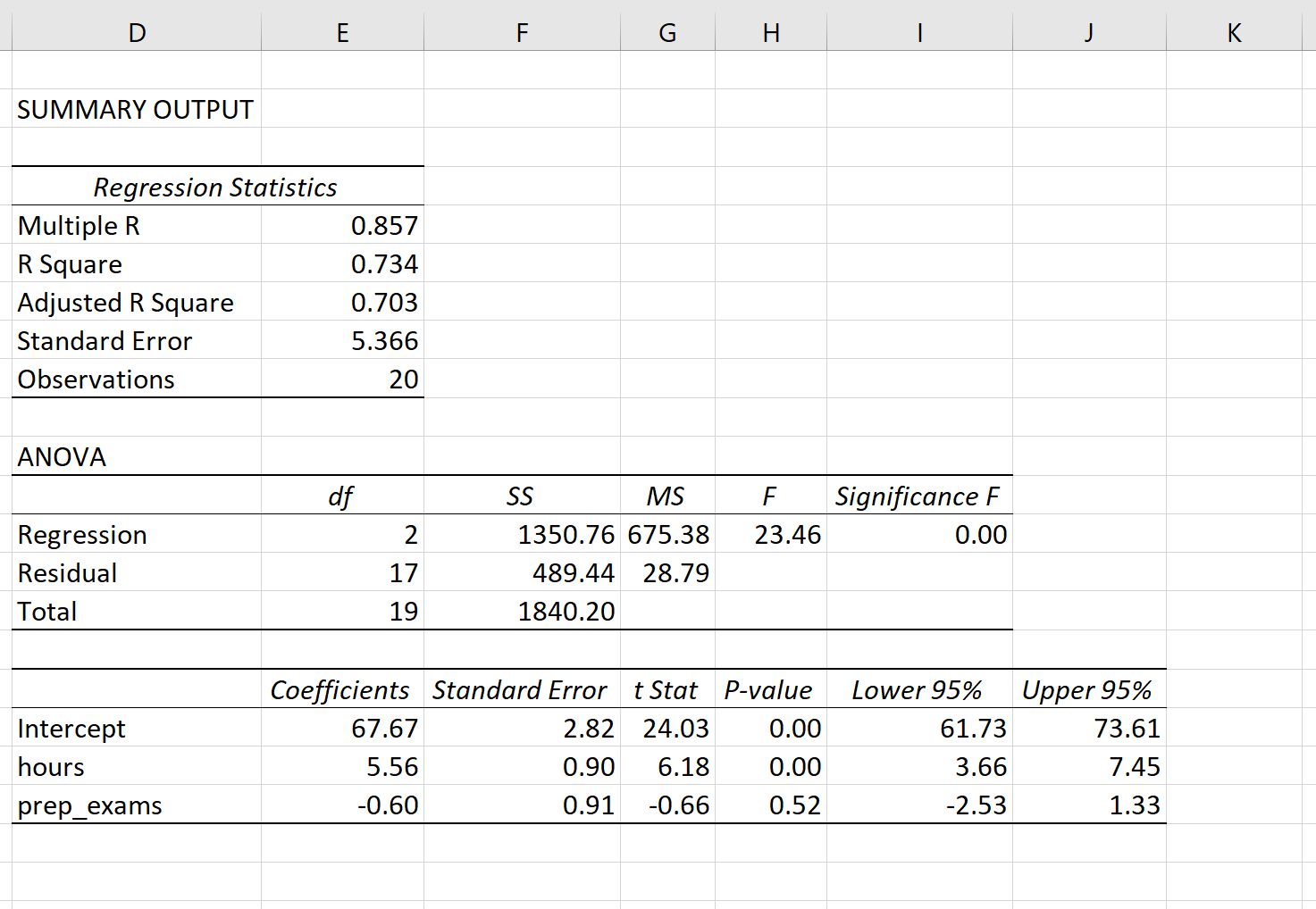
1. Using Statistical Software
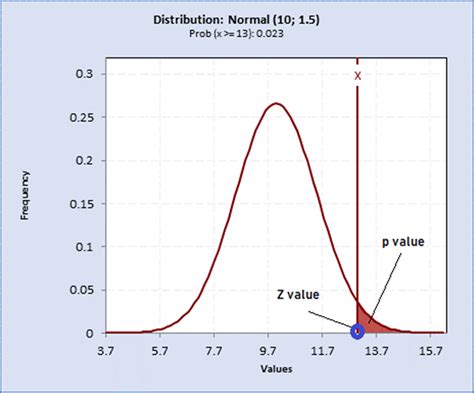
One of the most common and efficient ways to calculate the p-value is by using statistical software such as R, SPSS, SAS, or Python libraries like SciPy and Statsmodels. These programs can perform complex statistical calculations quickly and accurately, including hypothesis testing. For example, in R, one can use the
t.test() function for t-tests or lm() for linear regression analysis, both of which can provide p-values for the hypotheses being tested.
- Advantages: Easy to use, rapid calculation, and ability to handle large datasets.
- Disadvantages: Requires access to the software and basic knowledge of how to use it.
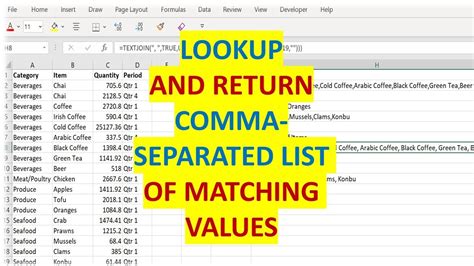
2. Online P-Value Calculators

For those without access to statistical software or preferring a more straightforward approach, online p-value calculators can be a convenient option. These web-based tools allow users to input their data or summary statistics and calculate the p-value for various statistical tests. They are particularly useful for simple calculations and educational purposes.
- Advantages: Accessibility, ease of use, and no need for software installation.
- Disadvantages: Limited functionality compared to full statistical software packages, and caution is needed regarding data privacy.
3. Manual Calculation
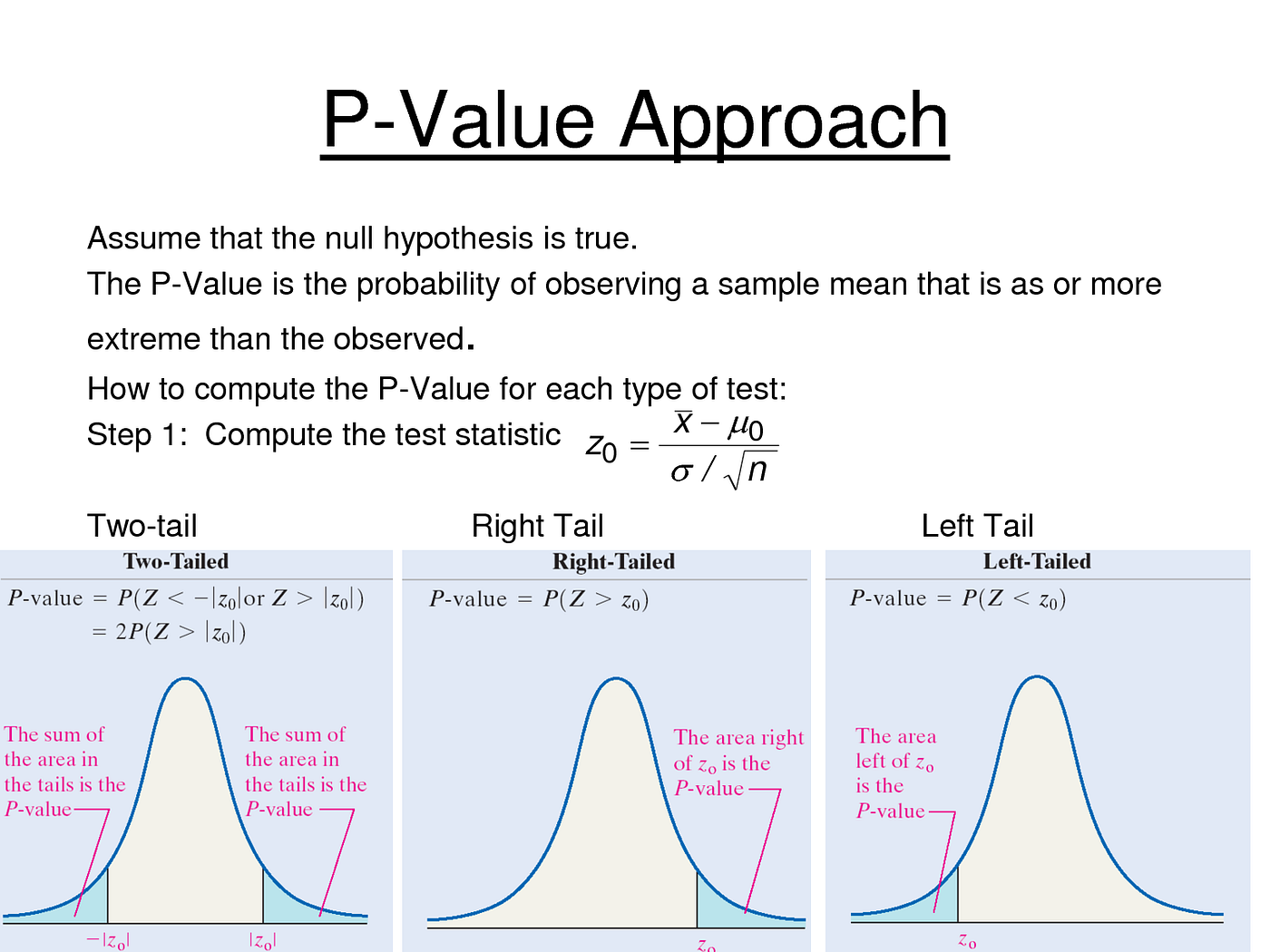
In some cases, particularly for educational purposes or when working with very simple datasets, it might be beneficial to calculate the p-value manually. This involves understanding the statistical test being applied (e.g., t-test, ANOVA) and applying the relevant formulae. Manual calculation can provide a deeper understanding of the statistical principles involved.
- Advantages: Enhances understanding of statistical concepts.
- Disadvantages: Time-consuming, prone to error, and not practical for large datasets.
4. Using a Graphing Calculator
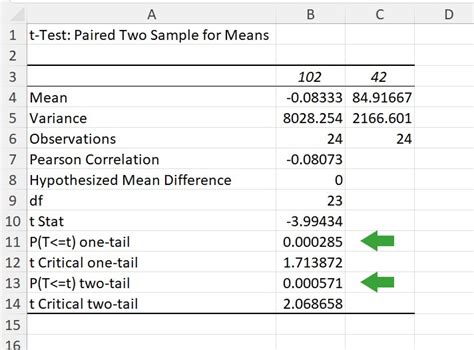
Some graphing calculators, especially those designed for statistics like the TI-83 or TI-84, have built-in functions for statistical analysis, including hypothesis testing. These calculators can calculate p-values for common tests, making them a useful tool for students or in situations where access to a computer is limited.
- Advantages: Portable, easy to use for simple analyses, and useful for educational settings.
- Disadvantages: Limited in their statistical capabilities compared to software, and the user interface might be less intuitive for complex analyses.
5. Spreadsheet Software
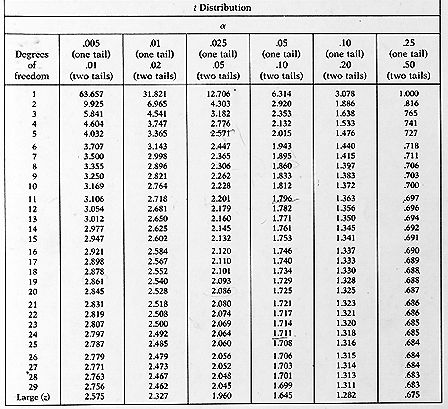
Spreadsheet software like Microsoft Excel or Google Sheets can also be used to calculate p-values, either through built-in functions or by implementing statistical formulas manually. For instance, Excel has a
T.TEST function for calculating the p-value of a t-test. This method is versatile and can be particularly useful for those already familiar with spreadsheet applications.
- Advantages: Widely available, flexible, and can be used for both data organization and analysis.
- Disadvantages: May require more effort to set up compared to dedicated statistical software, and built-in statistical functions might be limited.
💡 Note: Regardless of the method chosen, it's essential to understand the underlying statistical concepts and the assumptions of the test being performed to interpret the p-value correctly.
Interpreting P-Values
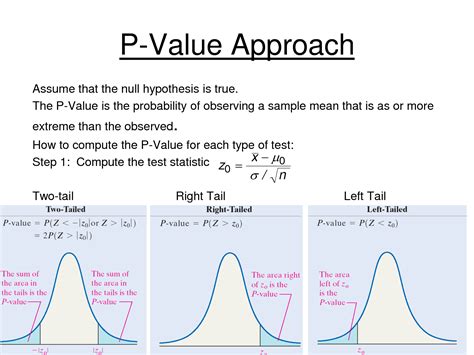
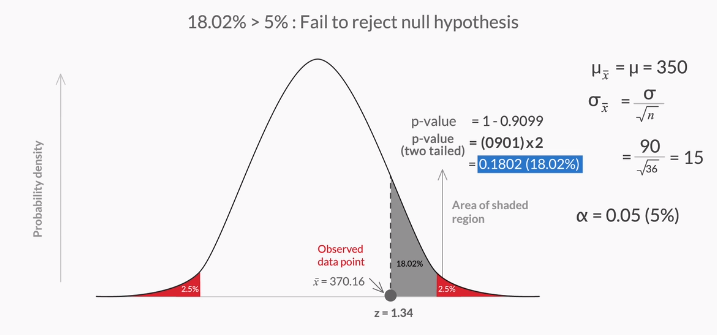
Once the p-value is obtained, interpreting it correctly is crucial. A small p-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, suggesting that the null hypothesis can be rejected in favor of the alternative hypothesis. However, the p-value does not indicate the importance or size of the effect; for this, metrics like effect size are necessary.
| P-Value | Interpretation |
|---|---|
| p < 0.05 | Reject the null hypothesis |
| p ≥ 0.05 | Fail to reject the null hypothesis |

To enhance understanding and application of p-values, it’s also important to consider: - Type I errors (rejecting a true null hypothesis) and Type II errors (failing to reject a false null hypothesis). - The power of a test, which is the probability that it correctly rejects a false null hypothesis. - Confidence intervals, which provide a range of values within which the true parameter is likely to lie.
In summary, calculating the p-value is a critical step in statistical hypothesis testing, and various methods are available to achieve this, each with its advantages and limitations. Understanding the p-value and its interpretation is essential for drawing meaningful conclusions from data analysis.
What does a p-value of 0.05 mean?

+
A p-value of 0.05 means that there is a 5% probability of observing the results (or more extreme) assuming that the null hypothesis is true. It is commonly used as a threshold for significance, where a p-value below 0.05 leads to the rejection of the null hypothesis.
How do I choose the right method for calculating the p-value?
+
The choice of method depends on the complexity of the analysis, the type of data, and personal preference or familiarity with software. For simple analyses, online calculators or spreadsheet functions might suffice, while more complex analyses may require dedicated statistical software.
What are common misconceptions about p-values?
+
Common misconceptions include believing that the p-value measures the probability that the null hypothesis is true, or that a p-value below 0.05 necessarily indicates a significant or important effect. It’s also misunderstood as the probability of the data given the null hypothesis, rather than the probability of the test statistic (or more extreme) given the null hypothesis.