5 Ways To Find Z Stat
Introduction to Z Statistic
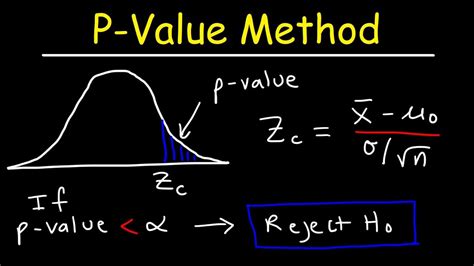
The Z statistic, also known as a Z score, is a statistical measure that describes a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean. If a value has a Z score of 0, it is equal to the mean. A positive Z score indicates that the value is above the mean, while a negative Z score indicates that it is below the mean. The Z statistic is widely used in hypothesis testing and confidence intervals.
Understanding the Z Statistic Formula

The formula for calculating the Z statistic is Z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation. This formula provides a way to compare different data points from the same data set or to compare data points from different datasets.
5 Ways to Find the Z Statistic
There are several methods to find the Z statistic, depending on the context and available data. Here are five common ways:
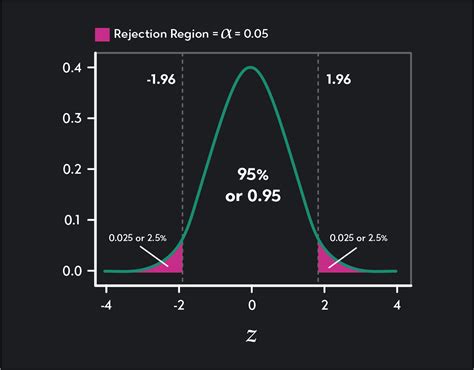
- Using a Z Table or Standard Normal Distribution Table: A Z table is a table that shows the probability of obtaining a value less than or equal to a given Z score. By looking up the Z score in the table, you can find the corresponding probability. This method is useful when you have the Z score and want to find the probability.
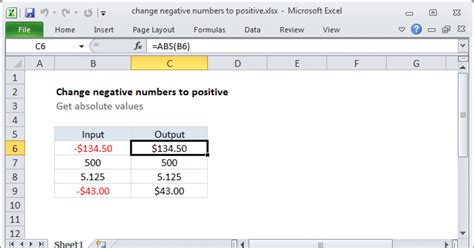
- Calculating from Raw Data: If you have the raw data, you can calculate the Z statistic using the formula Z = (X - μ) / σ. This involves finding the mean and standard deviation of the data set, then plugging in the values into the formula.
- Using a Statistical Calculator or Software: Many statistical calculators and software packages, such as R or Python, have built-in functions to calculate the Z statistic. These tools can save time and reduce errors.
- Converting from Other Statistics: In some cases, you can convert other statistics, such as a t statistic or a chi-squared statistic, to a Z statistic. This requires knowledge of the relationships between different statistical measures.
- Using Online Z Score Calculators: There are many online tools and calculators that can calculate the Z statistic for you. These tools often require you to input the value, mean, and standard deviation, and then provide the calculated Z score.
Example Calculation of Z Statistic
Suppose we have a dataset with a mean of 10 and a standard deviation of 2. We want to find the Z score of a value of 12. Using the formula Z = (X - μ) / σ, we get: Z = (12 - 10) / 2 = 2 / 2 = 1. This means that the value of 12 is one standard deviation above the mean.
Importance of Z Statistic in Real-World Applications
The Z statistic has many real-world applications, including:
- Quality Control: The Z statistic can be used to monitor the quality of products in a manufacturing process. By calculating the Z score of a product’s characteristics, such as its length or weight, manufacturers can determine if the product is within the acceptable range.
- Medical Research: The Z statistic is used in medical research to compare the means of different groups, such as the mean blood pressure of patients with and without a certain disease.
- Finance: The Z statistic is used in finance to evaluate the performance of investment portfolios. By calculating the Z score of a portfolio’s returns, investors can determine if the portfolio is performing better or worse than expected.
📝 Note: The Z statistic is sensitive to outliers, so it's essential to check for outliers before calculating the Z score.
Common Mistakes to Avoid When Calculating Z Statistic

When calculating the Z statistic, there are several common mistakes to avoid:
- Forgetting to calculate the standard deviation: The standard deviation is a critical component of the Z statistic formula. Forgetting to calculate it can lead to incorrect results.
- Using the wrong mean or standard deviation: Make sure to use the correct mean and standard deviation for the dataset. Using the wrong values can lead to incorrect results.
- Not checking for outliers: Outliers can affect the accuracy of the Z statistic. It’s essential to check for outliers before calculating the Z score.
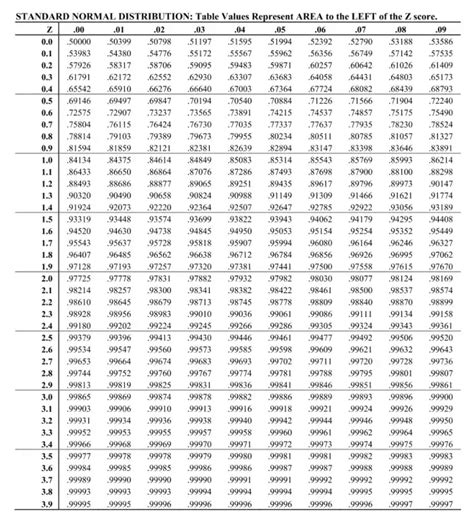
| Z Score | Probability |
|---|---|
| -1 | 0.1587 |
| 0 | 0.5 |
| 1 | 0.8413 |

In summary, the Z statistic is a powerful tool for comparing values to the mean of a dataset. By understanding the formula and common methods for calculating the Z statistic, you can apply it to a wide range of real-world problems.
What is the Z statistic used for?

+
The Z statistic is used to compare a value to the mean of a dataset. It is widely used in hypothesis testing and confidence intervals.
How do I calculate the Z statistic?

+
The Z statistic can be calculated using the formula Z = (X - μ) / σ, where X is the value, μ is the mean, and σ is the standard deviation.
What are some common mistakes to avoid when calculating the Z statistic?

+
Common mistakes to avoid include forgetting to calculate the standard deviation, using the wrong mean or standard deviation, and not checking for outliers.
In final thoughts, mastering the Z statistic is essential for anyone working with data. By understanding the formula, common methods, and real-world applications, you can unlock the power of the Z statistic and make informed decisions. Whether you’re working in quality control, medical research, or finance, the Z statistic is a valuable tool that can help you achieve your goals.