5 Ways To Z Score

Introduction to Z Scores

In statistics, a Z score, also known as a standard score, is a measure of how many standard deviations an element is from the mean. Z scores are used to compare the results of different datasets or to identify outliers in a dataset. Calculating Z scores can be done in various ways, depending on the information provided and the tools available. This article will explore five ways to calculate Z scores, including using formulas, online calculators, statistical software, programming languages, and a Z score table.
Method 1: Calculating Z Score Using a Formula

The most basic way to calculate a Z score is by using the Z score formula. The formula for calculating a Z score is: Z = (X - μ) / σ Where: - Z is the Z score - X is the value of the element - μ is the mean of the dataset - σ is the standard deviation of the dataset For example, if you want to calculate the Z score of a value X = 80, with a mean μ = 70 and a standard deviation σ = 10, you can plug these values into the formula: Z = (80 - 70) / 10 = 10 / 10 = 1 This means that the value X = 80 is 1 standard deviation above the mean.
Method 2: Using Online Z Score Calculators

Another way to calculate Z scores is by using online Z score calculators. These calculators are readily available on the internet and can be used for free. To use an online Z score calculator, you simply need to enter the value of the element, the mean, and the standard deviation, and the calculator will compute the Z score for you. Online calculators are convenient and can save you time, especially when dealing with large datasets.
Method 3: Calculating Z Score Using Statistical Software
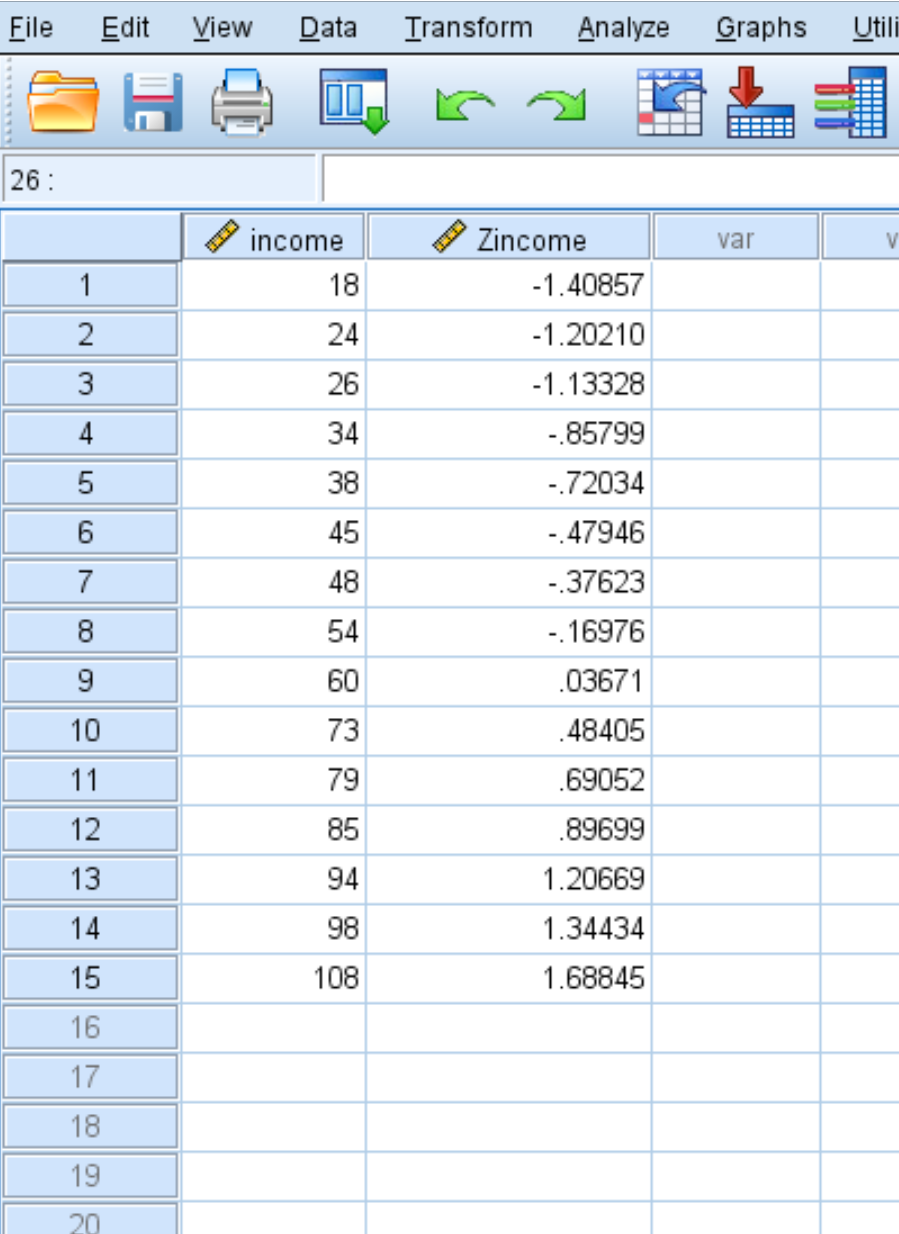
Statistical software such as R, Python, or SPSS can also be used to calculate Z scores. These software programs have built-in functions for calculating Z scores, making it easy to compute Z scores for large datasets. For example, in R, you can use the following code to calculate a Z score:
z_score <- function(x, mu, sigma) {
z <- (x - mu) / sigma
return(z)
}
You can then call this function with your values to get the Z score.
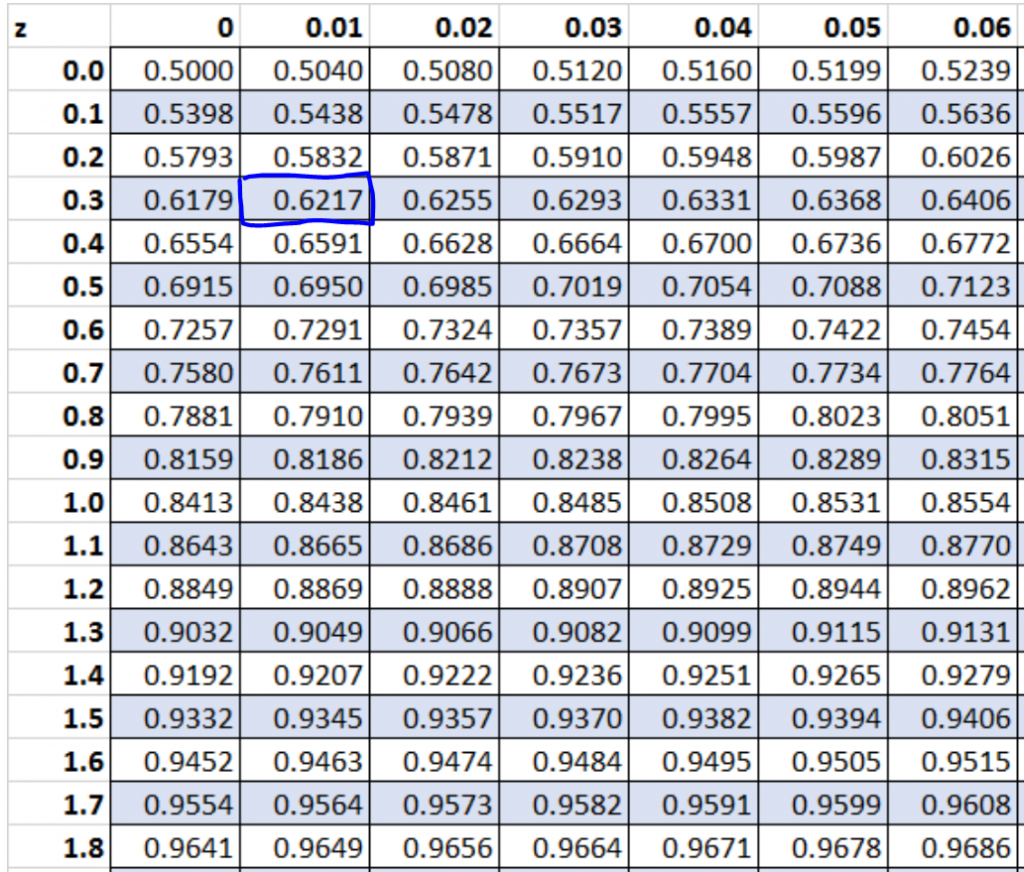
Method 4: Using a Z Score Table
A Z score table, also known as a standard normal distribution table, is a table that shows the probability that a random variable with a normal distribution will have a value less than or equal to a given Z score. To use a Z score table, you need to calculate the Z score first, and then look up the corresponding probability in the table. Z score tables are useful when you need to find the probability of a value occurring, given its Z score.
Method 5: Calculating Z Score Using a Programming Language
Finally, you can also calculate Z scores using programming languages such as Python or Java. These languages have libraries and functions that can be used to calculate Z scores. For example, in Python, you can use the following code to calculate a Z score:
import numpy as np
def calculate_z_score(x, mu, sigma):
z = (x - mu) / sigma
return z
x = 80
mu = 70
sigma = 10
z = calculate_z_score(x, mu, sigma)
print(z)
This code defines a function calculate_z_score that takes the value, mean, and standard deviation as input, calculates the Z score, and returns it.
📝 Note: When calculating Z scores, it's essential to ensure that the mean and standard deviation are calculated correctly, as incorrect values can lead to inaccurate Z scores.
In conclusion, calculating Z scores can be done in various ways, depending on the tools and resources available. Whether you use a formula, online calculator, statistical software, Z score table, or programming language, understanding how to calculate Z scores is essential in statistics and data analysis. By mastering these methods, you can efficiently compare datasets, identify outliers, and make informed decisions based on data.
What is a Z score, and why is it important in statistics?

+
A Z score is a measure of how many standard deviations an element is from the mean. It’s essential in statistics because it allows for the comparison of different datasets and helps identify outliers.
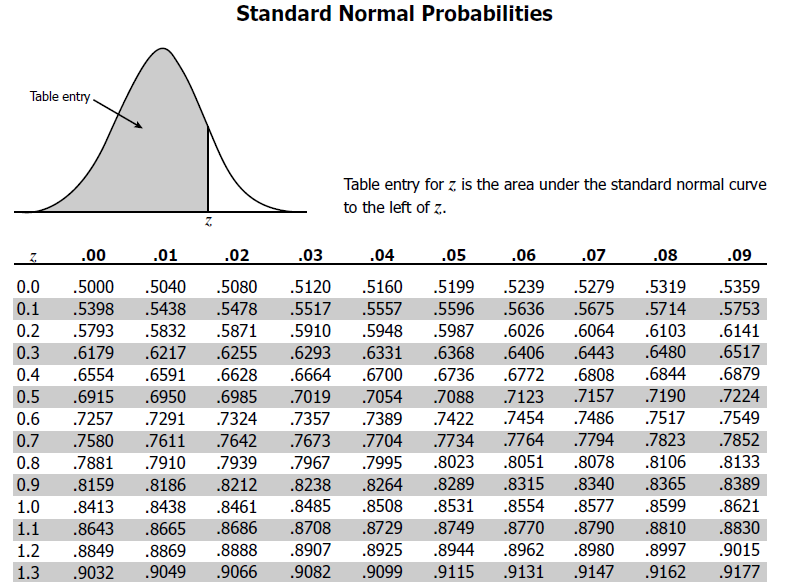
How do I calculate a Z score using a formula?
+
To calculate a Z score using a formula, you need to know the value of the element, the mean, and the standard deviation. The formula is Z = (X - μ) / σ, where Z is the Z score, X is the value, μ is the mean, and σ is the standard deviation.
What are some common applications of Z scores in real-life scenarios?
+
Z scores have various applications in real-life scenarios, including quality control, medical research, finance, and education. They help identify outliers, compare datasets, and make informed decisions based on data.
Can I use online calculators to calculate Z scores, and are they reliable?

+
Yes, you can use online calculators to calculate Z scores. They are convenient and can save you time. Most online calculators are reliable, but it’s essential to double-check the calculations to ensure accuracy.
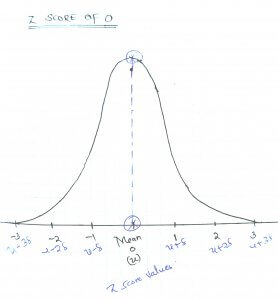
How do I interpret a Z score, and what does it tell me about the data?
+
A Z score tells you how many standard deviations an element is from the mean. A positive Z score indicates that the value is above the mean, while a negative Z score indicates that the value is below the mean. The absolute value of the Z score tells you how many standard deviations away from the mean the value is.