5 Ways To Get P Value

Introduction to P-Value

The p-value, or probability value, is a key concept in statistical hypothesis testing, representing the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. The calculation and interpretation of p-values are crucial in determining the significance of the results in various fields, including medicine, social sciences, and physics. In this article, we will explore five ways to get the p-value, highlighting the methods, applications, and interpretations.

Understanding P-Value

Before diving into the methods of obtaining p-values, it’s essential to understand what a p-value represents. A small p-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, leading to the rejection of the null hypothesis. On the other hand, a large p-value suggests that the data are consistent with the null hypothesis, and thus, we fail to reject it.

Method 1: Using Statistical Software

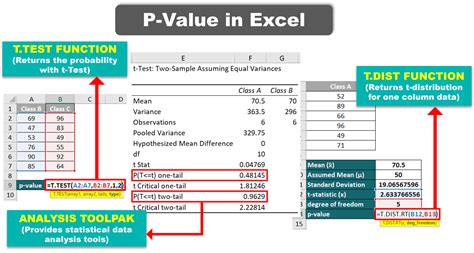
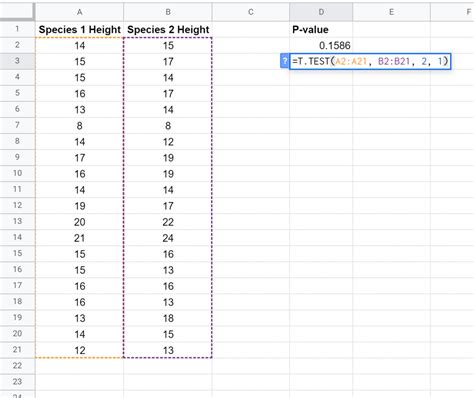
One of the most common methods to obtain p-values is by using statistical software such as R, Python, or SPSS. These programs have built-in functions for various statistical tests (e.g., t-test, ANOVA, regression) that calculate and report p-values directly. For example, in R, the t.test() function performs a t-test and returns the p-value, while in Python, libraries like SciPy and Statsmodels provide similar functionality.

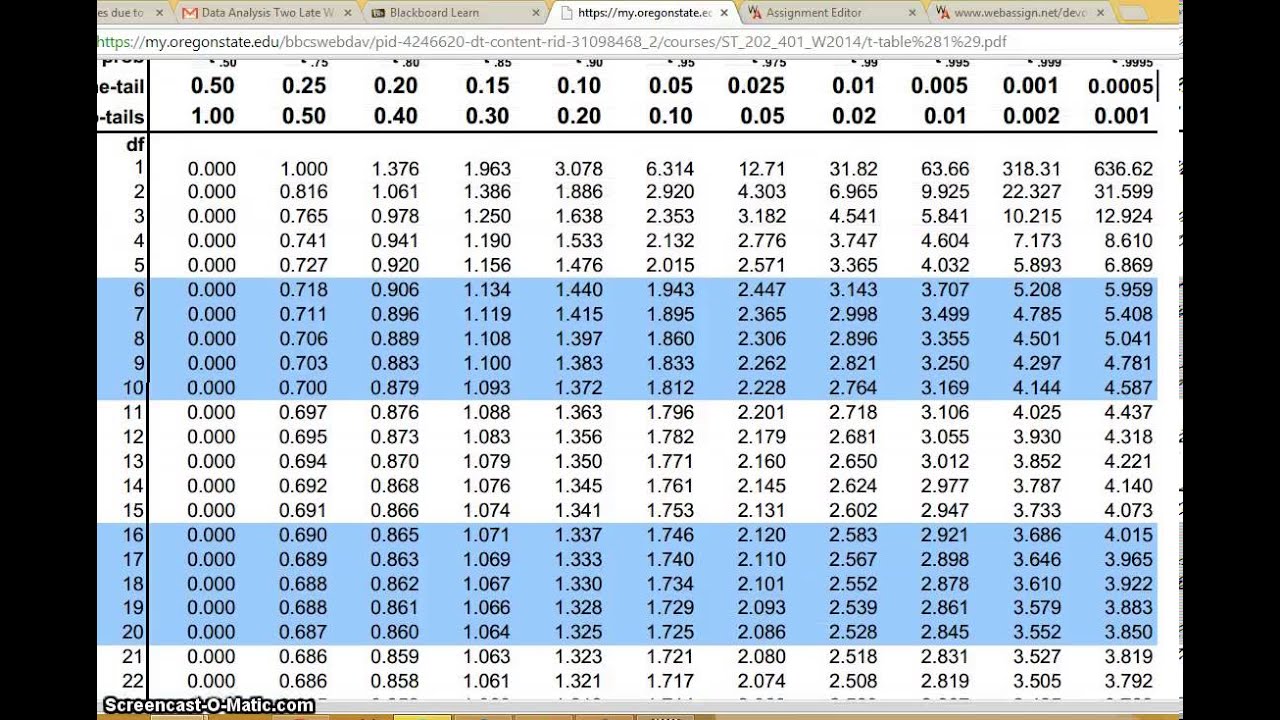
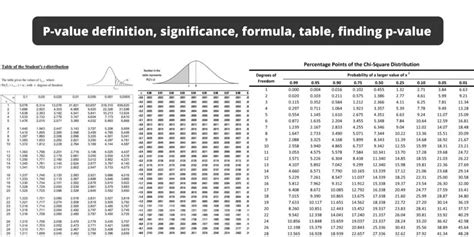
Method 2: Consulting Statistical Tables

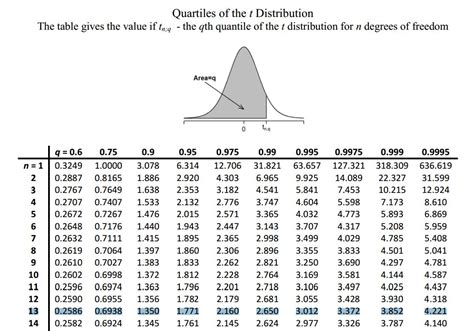
Another method, although less common with the advent of computational tools, is consulting statistical tables. These tables, found in the back of many statistics textbooks, provide critical values for various statistical tests. By looking up the critical value for a given test statistic and degrees of freedom, one can determine the p-value. This method is more manual and less precise than using software but can be useful for quick estimates or when computational tools are not available.

Method 3: Online P-Value Calculators

There are numerous online tools and calculators that can compute p-values for various statistical tests. These tools are convenient for quick calculations and often require input of the test statistic and degrees of freedom. They can be particularly useful for students or researchers who need a rapid p-value calculation without accessing full statistical software.

Method 4: Manual Calculation

For those interested in the underlying mathematics, p-values can be calculated manually using the appropriate statistical distribution (e.g., t-distribution, F-distribution). This method involves calculating the test statistic and then finding the probability of observing a value at least as extreme as the one observed, using the distribution’s cumulative distribution function (CDF). While educational, manual calculation is generally impractical for most research applications due to its complexity and the potential for error.

Method 5: Bootstrap Resampling

Bootstrap resampling is a computational method that can be used to estimate p-values, especially in situations where traditional parametric methods are not applicable. The basic idea is to resample the data with replacement many times, calculate the test statistic for each resample, and then determine the proportion of these test statistics that are at least as extreme as the one observed in the original data. This proportion serves as an estimate of the p-value.

📝 Note: Bootstrap resampling is particularly useful for complex data sets or when the distribution of the test statistic is unknown.

Interpretation of P-Values

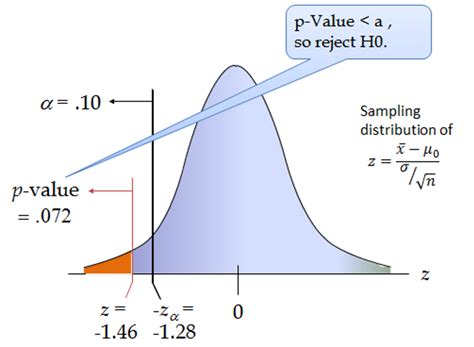
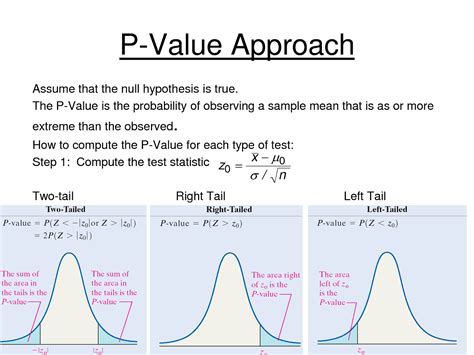
Regardless of the method used to obtain the p-value, its interpretation remains crucial. A p-value below a certain significance level (commonly 0.05) leads to the rejection of the null hypothesis, suggesting that the observed effect is statistically significant. However, it’s essential to remember that p-values do not measure the size or importance of an effect; for this, effect sizes and confidence intervals are more informative.

Method	Description	Advantages	Disadvantages
Statistical Software	Using R, Python, or SPSS for calculations	Accurate, efficient, and versatile	Requires access to software and basic programming skills
Statistical Tables	Consulting tables for critical values	Quick estimates, no software needed	Less precise, limited applicability
Online Calculators	Using web tools for p-value calculations	Convenient, quick, and easy to use	Limited to specific tests, may lack precision
Manual Calculation	Calculating p-values using statistical distributions	Educational, understands underlying math	Complex, prone to errors, impractical
Bootstrap Resampling	Estimating p-values through resampling	Useful for complex data, non-parametric	Computationally intensive, may require programming

In summary, obtaining p-values is a fundamental step in statistical hypothesis testing, and various methods are available, ranging from the use of statistical software and online calculators to manual calculations and bootstrap resampling. Each method has its advantages and disadvantages, and the choice of method depends on the specific research question, the nature of the data, and the resources available. Understanding the concept of p-values and how to obtain them is crucial for making informed decisions in research and applied statistics.