5 Ways To Calculate Average Percentage
Introduction to Average Percentage Calculation
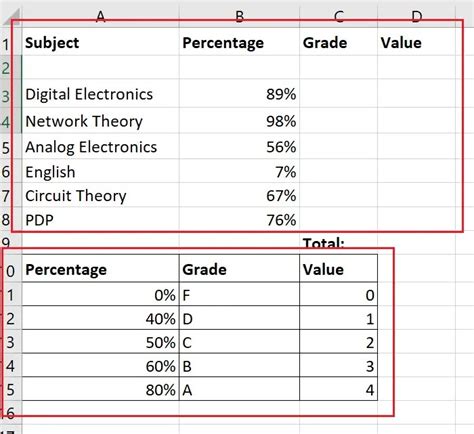
Calculating the average percentage is a crucial skill in various fields, including finance, education, and data analysis. The average percentage provides a clear understanding of the overall performance or trend. In this blog post, we will explore five different methods to calculate the average percentage, each with its own application and significance. Understanding these methods will help you make informed decisions and analyze data more effectively.
Method 1: Simple Average Percentage Calculation
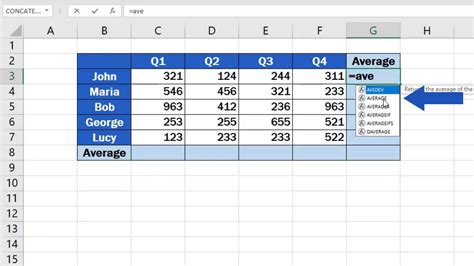
The simplest way to calculate the average percentage is by adding all the percentages and then dividing by the total number of values. This method is useful when all the percentages have equal weightage. For example, if you want to calculate the average percentage of marks obtained by a student in five subjects, you add the percentages of all five subjects and then divide by 5.
Method 2: Weighted Average Percentage Calculation

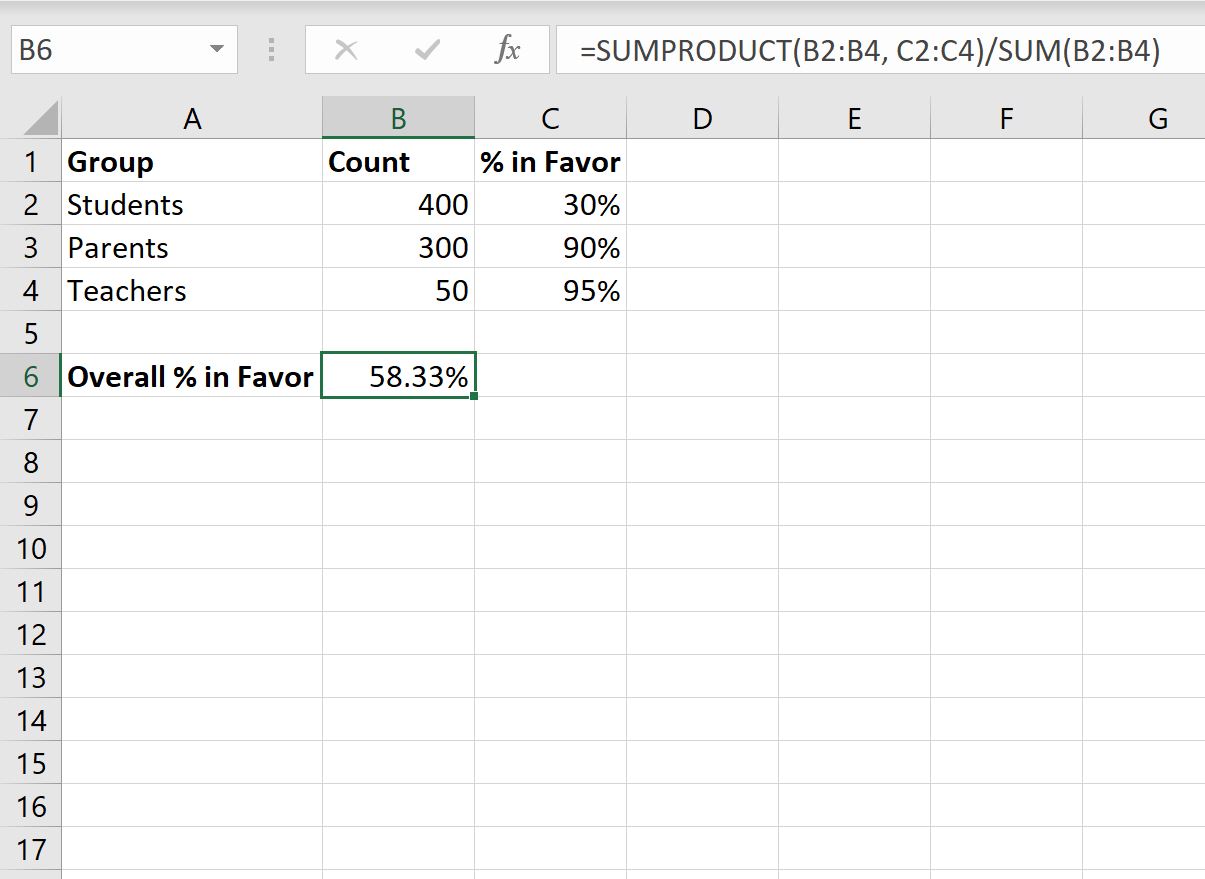
In situations where the percentages have different weightages, the weighted average method is more appropriate. This method involves multiplying each percentage by its respective weightage, adding these products, and then dividing by the sum of all weightages. For instance, if you are calculating the average percentage of a student’s grades, where different subjects have different credit points, you would use the weighted average method to get a more accurate representation.
Method 3: Geometric Average Percentage Calculation
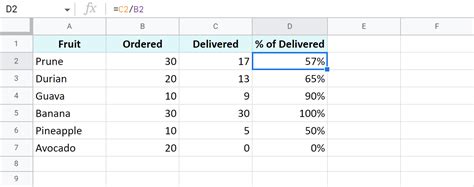
The geometric average method is used for calculating the average percentage when the percentages represent growth rates or ratios. This method involves converting the percentages into ratios, finding their geometric mean, and then converting back to a percentage. The geometric average is particularly useful in finance for calculating the average rate of return on investments over multiple periods.
Method 4: Harmonic Average Percentage Calculation
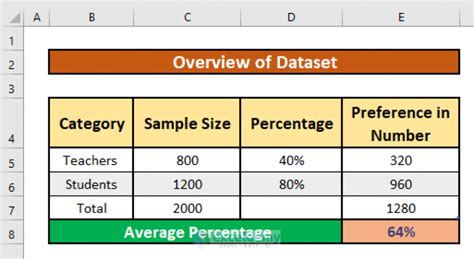
The harmonic average is another method used for calculating the average percentage, especially when dealing with rates or ratios. It is calculated by finding the reciprocal of the arithmetic mean of the reciprocals of the percentages. The harmonic average is useful in situations where the percentages represent rates, such as the average speed of a vehicle over different distances.
Method 5: Median Average Percentage Calculation
The median average method involves arranging the percentages in ascending or descending order and finding the middle value. If there is an even number of percentages, the median is the average of the two middle values. The median average is useful for identifying the central tendency when the data set contains outliers that might skew the mean.
📝 Note: Understanding the context and choosing the appropriate method for calculating the average percentage is crucial for accurate analysis and interpretation of data.
Comparison of Average Percentage Calculation Methods
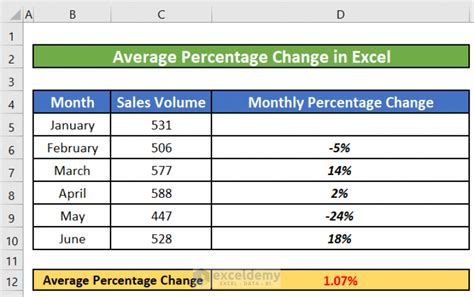
Each method has its application and provides a different insight into the data. The choice of method depends on the nature of the data, the purpose of the analysis, and the presence of weightages or outliers. Comparing these methods can help in selecting the most suitable one for a given scenario.
| Method | Description | Application |
|---|---|---|
| Simple Average | Add all percentages and divide by the number of values. | Equal weightage percentages. |
| Weighted Average | Multiply each percentage by its weightage, add, and divide by the sum of weightages. | Different weightages for percentages. |
| Geometric Average | Find the geometric mean of the percentages. | Growth rates or ratios. |
| Harmonic Average | Find the reciprocal of the arithmetic mean of the reciprocals. | Rates or ratios. |
| Median Average | Find the middle value of ordered percentages. | Outliers in the data set. |

In summary, calculating the average percentage is not a one-size-fits-all approach. Different scenarios require different methods to ensure accurate and meaningful analysis. By understanding and applying these five methods appropriately, individuals can better analyze data, make informed decisions, and achieve their objectives more effectively.
What is the simplest method to calculate the average percentage?
+
The simplest method to calculate the average percentage is the simple average method, where all percentages are added and then divided by the total number of values.
When should the weighted average method be used?

+
The weighted average method should be used when the percentages have different weightages or importance levels.
What is the purpose of calculating the average percentage?

+
The purpose of calculating the average percentage is to understand the overall trend or performance, which is crucial for decision-making and analysis in various fields.