5 Ways To Factorial

Introduction to Factorial

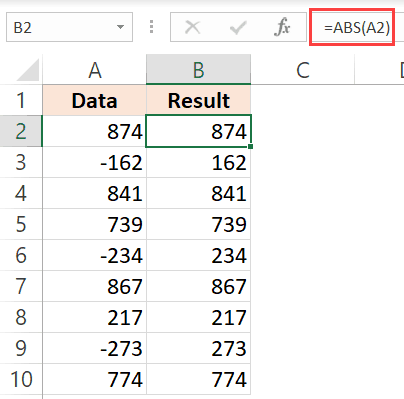
The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example, 5! = 5*4*3*2*1 = 120. Calculating the factorial of a number can be done in several ways, including using recursion, iteration, dynamic programming, memoization, and math libraries. In this article, we will explore these different methods to calculate the factorial of a number.

Method 1: Recursive Approach

The recursive approach involves defining a function that calls itself to calculate the factorial. The base case for this function is when the input number is 0 or 1, in which case the function returns 1. For any other number, the function calls itself with the argument decremented by 1 and multiplies the result by the current number. Here are the steps to calculate the factorial using recursion: * Define a function that takes an integer as input. * Check if the input number is 0 or 1. If so, return 1. * Otherwise, call the function with the argument decremented by 1 and multiply the result by the current number. * Return the final result.

Method 2: Iterative Approach

The iterative approach involves using a loop to calculate the factorial. This method is more efficient than the recursive approach, especially for large numbers, since it avoids the overhead of function calls. Here are the steps to calculate the factorial using iteration: * Initialize a variable to 1. * Loop from 1 to the input number. * In each iteration, multiply the variable by the current number. * Return the final result.

Method 3: Dynamic Programming Approach

The dynamic programming approach involves storing the results of sub-problems to avoid redundant calculations. This method is useful when calculating the factorial of multiple numbers. Here are the steps to calculate the factorial using dynamic programming: * Create an array to store the factorial of each number up to the input number. * Initialize the first element of the array to 1. * Loop from 1 to the input number. * In each iteration, calculate the factorial by multiplying the previous result by the current number. * Store the result in the array. * Return the final result.

Method 4: Memoization Approach

The memoization approach involves storing the results of expensive function calls to avoid redundant calculations. This method is similar to dynamic programming, but it uses a cache to store the results instead of an array. Here are the steps to calculate the factorial using memoization: * Create a cache to store the factorial of each number. * Define a function that takes an integer as input. * Check if the input number is in the cache. If so, return the cached result. * Otherwise, calculate the factorial using recursion or iteration and store the result in the cache. * Return the final result.

Method 5: Math Library Approach

The math library approach involves using a pre-built library function to calculate the factorial. This method is the most efficient and accurate way to calculate the factorial, especially for large numbers. Here are the steps to calculate the factorial using a math library: * Import the math library. * Use the library function to calculate the factorial of the input number. * Return the final result.

📝 Note: The math library approach is not always available, and the implementation may vary depending on the programming language.

To illustrate the difference between these methods, consider the following table:

Method	Time Complexity	Space Complexity
Recursive	O(n)	O(n)
Iterative	O(n)	O(1)
Dynamic Programming	O(n)	O(n)
Memoization	O(n)	O(n)
Math Library	O(1)	O(1)

In summary, the choice of method depends on the specific requirements of the problem and the programming language being used. The recursive approach is simple but inefficient, while the iterative approach is more efficient but may not be suitable for large numbers. The dynamic programming and memoization approaches are useful when calculating the factorial of multiple numbers, while the math library approach is the most efficient and accurate way to calculate the factorial.

As we have seen, calculating the factorial of a number can be done in several ways, each with its own advantages and disadvantages. By understanding these different methods, we can choose the best approach for our specific needs and write more efficient and accurate code.