5 Ways To Do Exponent

Understanding Exponents

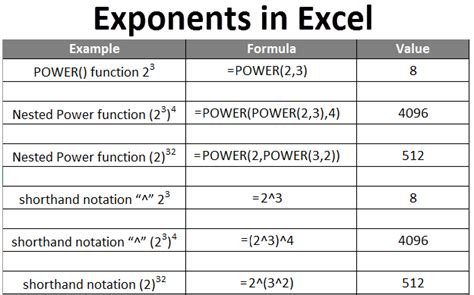
Exponents are a fundamental concept in mathematics, used to represent repeated multiplication of a number by itself. The base is the number being multiplied, and the exponent is the number of times it is multiplied. For example, in the expression 2^3, 2 is the base and 3 is the exponent, which means 2 \times 2 \times 2 = 8. In this blog post, we will explore five ways to calculate exponents.

Method 1: Manual Calculation

The most straightforward way to calculate an exponent is by manually multiplying the base by itself as many times as indicated by the exponent. This method is simple but can be time-consuming and prone to errors, especially for large exponents. - For small exponents, this method is feasible. - It helps in understanding the concept of exponents intuitively. - However, for large numbers, it becomes impractical.

Method 2: Using a Calculator

Most calculators have an exponent key, usually represented as x^y or a^b, which makes calculating exponents very easy. You simply enter the base, press the exponent key, enter the exponent, and press equals to get the result. - This method is quick and accurate. - It’s ideal for calculations involving large numbers. - However, it might not be helpful in understanding the underlying mathematical principles.

Method 3: Algebraic Manipulation

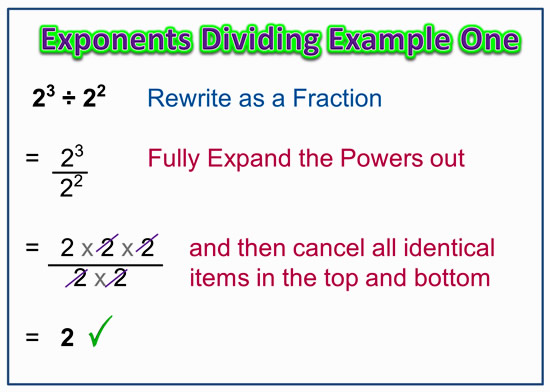
In some cases, especially in algebra and calculus, you might need to manipulate expressions containing exponents. This can involve using exponent rules such as a^m \cdot a^n = a^{m+n}, \frac{a^m}{a^n} = a^{m-n}, and (a^m)^n = a^{mn} to simplify expressions. - This method requires a good understanding of algebraic rules. - It’s essential for solving equations and simplifying complex expressions. - However, it can be challenging without a solid grasp of the rules.

Method 4: Using Logarithms

Logarithms are the inverse operation of exponents. While exponents ask “to what power must a base be raised to obtain a number?”, logarithms ask “to what power must a base be raised to obtain a number, and what is that power?”. Logarithms can be used to solve for the exponent in an equation where the base and result are known. - This method is particularly useful in solving equations where the exponent is the variable. - It requires understanding of logarithmic functions and their properties. - Logarithms can simplify complex exponential equations.

Method 5: Computational Software

With the advent of computational software and programming languages like Python, MATLAB, and R, calculating exponents has become even more straightforward. These tools not only can compute exponents quickly but also can handle very large numbers and are useful for repetitive calculations. - These tools are highly efficient and reduce the chance of human error. - They are indispensable for scientific and engineering applications. - However, basic understanding of programming or using the software is required.

💡 Note: Understanding the concept of exponents is crucial for any method you choose to calculate them. Whether you're using manual calculation, a calculator, algebraic manipulation, logarithms, or computational software, a solid grasp of what exponents represent will make your calculations more accurate and meaningful.

To summarize, calculating exponents can be approached in multiple ways, each with its own advantages and suited for different contexts. Whether it’s the simplicity of manual calculation, the precision of calculators, the elegance of algebraic manipulation, the utility of logarithms, or the power of computational software, choosing the right method depends on the specific problem you’re trying to solve and your personal preference or the requirements of the task at hand. Understanding the fundamentals of exponents and being proficient in multiple methods can make you more versatile and efficient in tackling mathematical and real-world problems.