5 Ways To Calculate Degrees

Introduction to Calculating Degrees

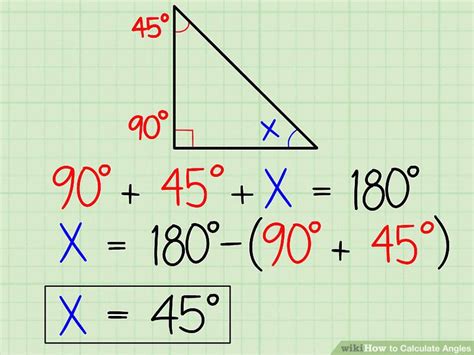
Calculating degrees is a fundamental concept in mathematics, particularly in trigonometry and geometry. It involves measuring angles in degrees, which is essential in various fields such as engineering, architecture, and physics. In this article, we will explore five ways to calculate degrees, including using trigonometric functions, angle addition, angle subtraction, complementary angles, and supplementary angles.

Method 1: Using Trigonometric Functions

Trigonometric functions such as sine, cosine, and tangent can be used to calculate degrees. These functions relate the ratios of the sides of a right triangle to the angles. For example, the sine of an angle is equal to the ratio of the opposite side to the hypotenuse. By using a calculator or trigonometric tables, we can find the degree measure of an angle given the ratio of the sides.

Method 2: Angle Addition

Angle addition involves adding two or more angles to find the resulting angle. This method is useful when we need to find the degree measure of a complex angle. For example, if we have two angles, 30° and 60°, we can add them to find the resulting angle: 30° + 60° = 90°. We can use this method to calculate degrees in various applications, such as finding the angle between two lines or the angle of elevation.

Method 3: Angle Subtraction

Angle subtraction involves subtracting one angle from another to find the resulting angle. This method is useful when we need to find the degree measure of an angle that is smaller than another angle. For example, if we have two angles, 90° and 30°, we can subtract them to find the resulting angle: 90° - 30° = 60°. We can use this method to calculate degrees in various applications, such as finding the angle between two lines or the angle of depression.

Method 4: Complementary Angles

Complementary angles are two angles whose sum is 90°. We can use this concept to calculate degrees by finding the complementary angle of a given angle. For example, if we have an angle of 60°, we can find its complementary angle by subtracting it from 90°: 90° - 60° = 30°. We can use this method to calculate degrees in various applications, such as finding the angle between two lines or the angle of elevation.

Method 5: Supplementary Angles

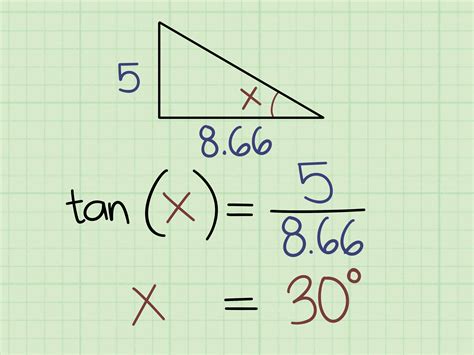
Supplementary angles are two angles whose sum is 180°. We can use this concept to calculate degrees by finding the supplementary angle of a given angle. For example, if we have an angle of 120°, we can find its supplementary angle by subtracting it from 180°: 180° - 120° = 60°. We can use this method to calculate degrees in various applications, such as finding the angle between two lines or the angle of depression.

📝 Note: When calculating degrees, it is essential to consider the unit of measurement and the context of the problem. We should always ensure that our calculations are accurate and relevant to the application.

To summarize the methods, we have: * Trigonometric functions: relate the ratios of the sides of a right triangle to the angles * Angle addition: add two or more angles to find the resulting angle * Angle subtraction: subtract one angle from another to find the resulting angle * Complementary angles: find the complementary angle of a given angle * Supplementary angles: find the supplementary angle of a given angle

In conclusion, calculating degrees is a crucial concept in mathematics, and there are various methods to do so. By understanding and applying these methods, we can solve problems in trigonometry, geometry, and other fields. Whether we are using trigonometric functions, angle addition, angle subtraction, complementary angles, or supplementary angles, we should always ensure that our calculations are accurate and relevant to the application.