5 Ways Chi Square Test
Introduction to Chi Square Test
The Chi Square test is a statistical method used to determine whether there is a significant association between two categorical variables. It is widely used in various fields such as medicine, social sciences, and marketing research. The test is particularly useful when dealing with categorical data, where the goal is to examine the relationship between two or more variables. In this article, we will explore five ways the Chi Square test can be applied in different contexts.
What is Chi Square Test?

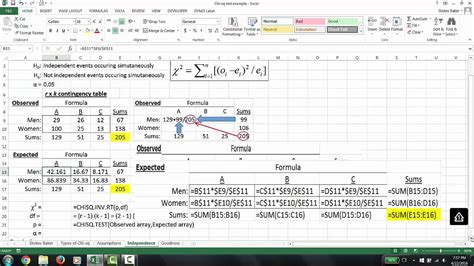
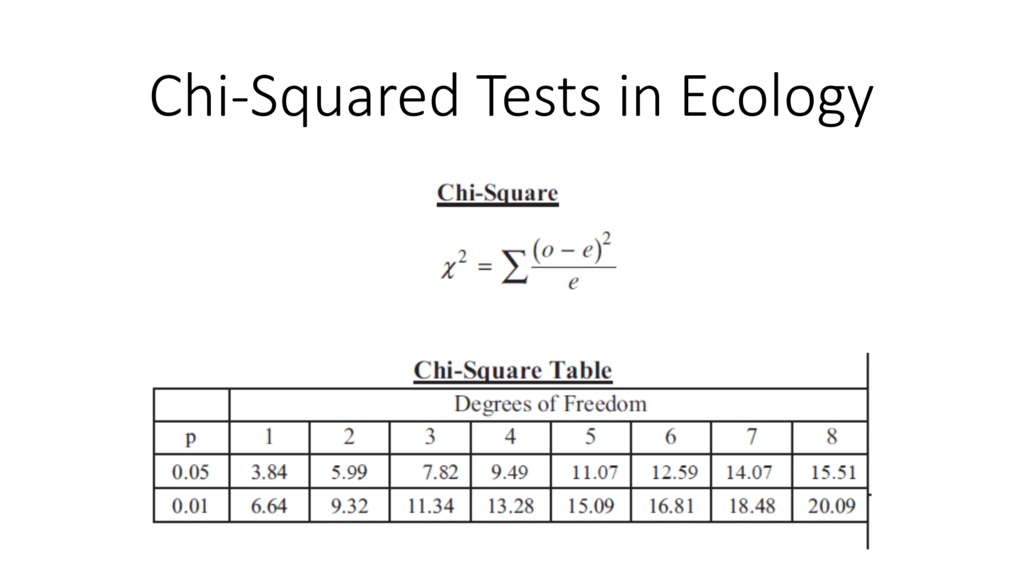
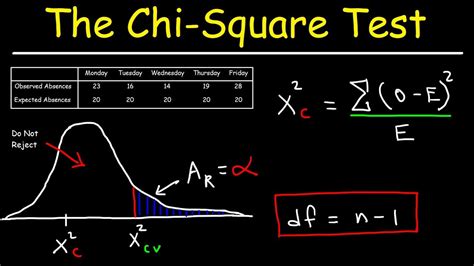
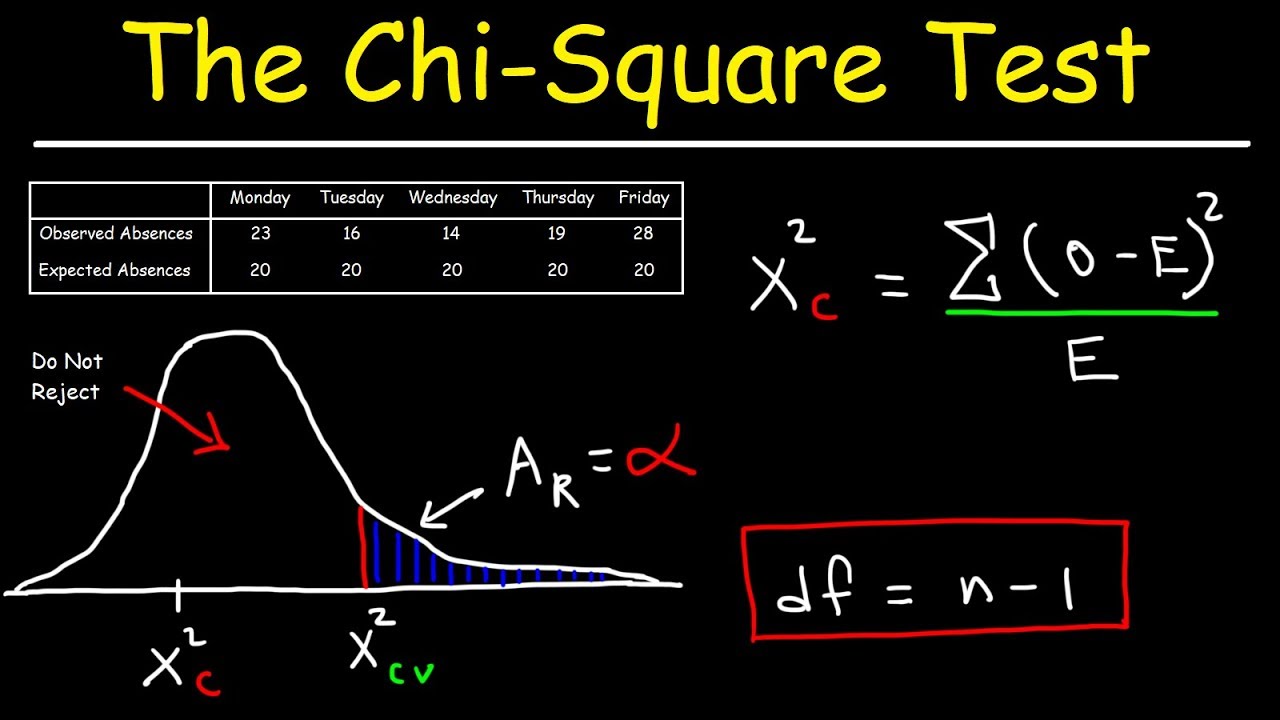
The Chi Square test, also known as the Chi Squared test or χ2 test, is a non-parametric test that compares the observed frequencies in one or more categories with the expected frequencies, assuming no association between the variables. The test calculates a statistic based on the difference between the observed and expected frequencies, which is then compared to a critical value from the Chi Square distribution. If the calculated statistic exceeds the critical value, the null hypothesis of no association is rejected, indicating a significant relationship between the variables.
5 Ways Chi Square Test is Used
Here are five ways the Chi Square test can be applied in different contexts:
- Testing for Independence: The Chi Square test can be used to determine whether two categorical variables are independent. For example, in a medical study, researchers might use the Chi Square test to examine whether there is a significant association between smoking status (smoker or non-smoker) and lung cancer diagnosis.
- Goodness of Fit: The Chi Square test can be used to evaluate how well a theoretical distribution fits a set of observed data. For instance, in a manufacturing process, the test can be used to determine whether the observed distribution of product defects matches the expected distribution.
- Homogeneity: The Chi Square test can be used to determine whether two or more populations have the same distribution of categorical variables. For example, in a social sciences study, researchers might use the Chi Square test to compare the distribution of educational attainment levels between different ethnic groups.
- Testing for Trends: The Chi Square test can be used to examine whether there is a significant trend in a categorical variable across different levels of another variable. For instance, in a marketing research study, the test can be used to determine whether there is a significant trend in customer satisfaction ratings across different product categories.
- Validation of Survey Instruments: The Chi Square test can be used to validate survey instruments by examining whether the observed responses match the expected responses. For example, in a psychology study, researchers might use the Chi Square test to evaluate whether a new survey instrument measures the intended construct.
How to Perform a Chi Square Test

To perform a Chi Square test, follow these steps: * State the Null and Alternative Hypotheses: The null hypothesis typically states that there is no significant association between the variables, while the alternative hypothesis states that there is a significant association. * Prepare the Data: The data should be in the form of a contingency table, where the rows and columns represent the different categories of the variables. * Calculate the Expected Frequencies: The expected frequencies are calculated based on the assumption of no association between the variables. * Calculate the Chi Square Statistic: The Chi Square statistic is calculated based on the difference between the observed and expected frequencies. * Determine the Degrees of Freedom: The degrees of freedom are determined based on the number of rows and columns in the contingency table. * Compare the Calculated Statistic to the Critical Value: If the calculated statistic exceeds the critical value, the null hypothesis is rejected, indicating a significant association between the variables.
📝 Note: The Chi Square test assumes that the observations are independent and that the categories are mutually exclusive. It is also important to check for assumptions such as no zero cells and no low expected frequencies.
Example of Chi Square Test
Suppose we want to examine whether there is a significant association between gender and favorite color. We collect data from a sample of 100 individuals and prepare the following contingency table:
| Favorite Color | Male | Female | Total |
|---|---|---|---|
| Red | 20 | 15 | 35 |
| Blue | 25 | 20 | 45 |
| Green | 10 | 10 | 20 |
| Total | 55 | 45 | 100 |

We calculate the expected frequencies and the Chi Square statistic, and determine that the calculated statistic exceeds the critical value. Therefore, we reject the null hypothesis and conclude that there is a significant association between gender and favorite color.
In summary, the Chi Square test is a powerful statistical method for examining the relationship between categorical variables. By understanding how to apply the test in different contexts, researchers and analysts can gain valuable insights into the relationships between variables and make informed decisions.
What is the main purpose of the Chi Square test?
+
The main purpose of the Chi Square test is to determine whether there is a significant association between two categorical variables.
What are the assumptions of the Chi Square test?

+
The Chi Square test assumes that the observations are independent and that the categories are mutually exclusive. It also assumes that there are no zero cells and no low expected frequencies.
How do I interpret the results of a Chi Square test?

+
If the calculated statistic exceeds the critical value, the null hypothesis is rejected, indicating a significant association between the variables. If the calculated statistic does not exceed the critical value, the null hypothesis is not rejected, indicating no significant association between the variables.