Find Critical Value In Excel

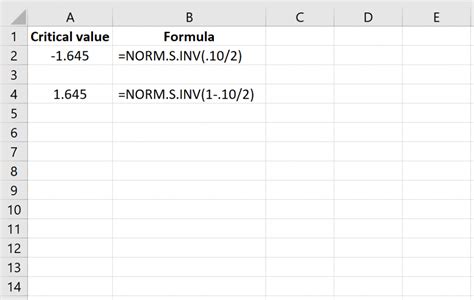
Understanding Critical Values in Excel

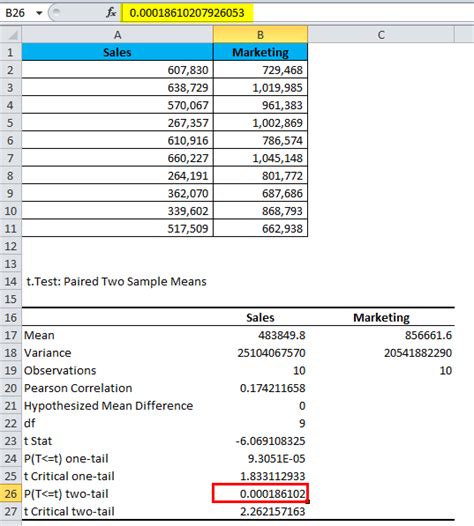
When working with statistical data in Excel, determining critical values is a crucial step in hypothesis testing. A critical value is a value in a statistical distribution that is used to determine whether a null hypothesis should be rejected or not. In this blog post, we will explore how to find critical values in Excel.

What are Critical Values?

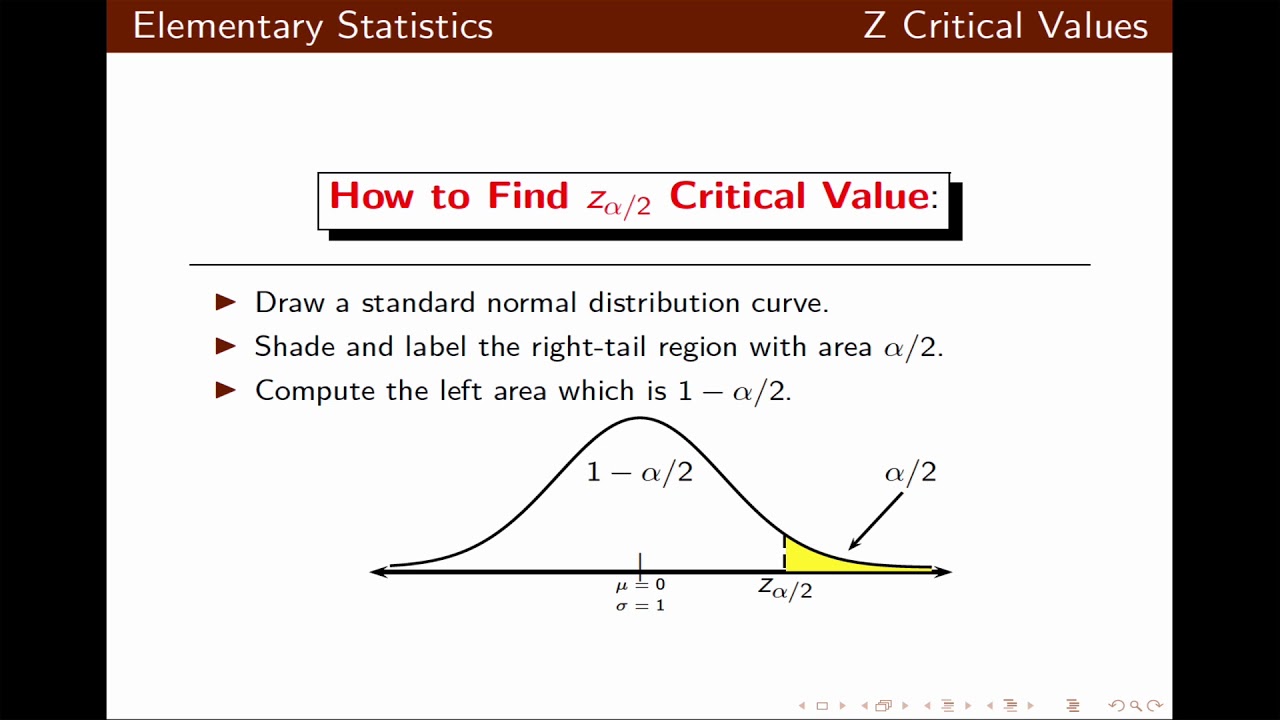
Critical values are the values of a test statistic that determine the boundaries of a rejection region. The rejection region is the area of the distribution where the null hypothesis is rejected. Critical values are typically denoted by the Greek letter alpha (α) and are usually set at 0.05, which means that there is a 5% chance of rejecting the null hypothesis when it is actually true.

How to Find Critical Values in Excel

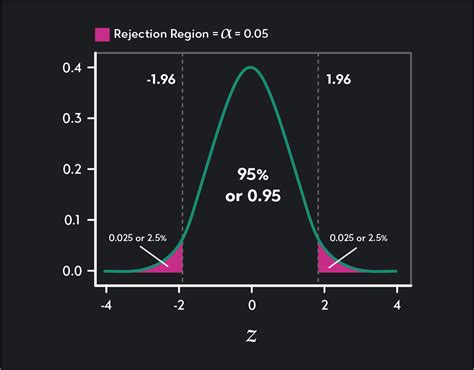
To find critical values in Excel, you can use the following methods:

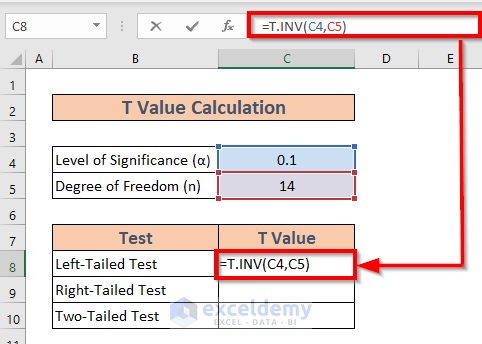
• Using the TINV Function: The TINV function in Excel returns the critical value from the t-distribution. The syntax for the TINV function is TINV(probability, degrees_of_freedom). For example, to find the critical value for a two-tailed test with a probability of 0.05 and 10 degrees of freedom, you would use the formula =TINV(0.05, 10).
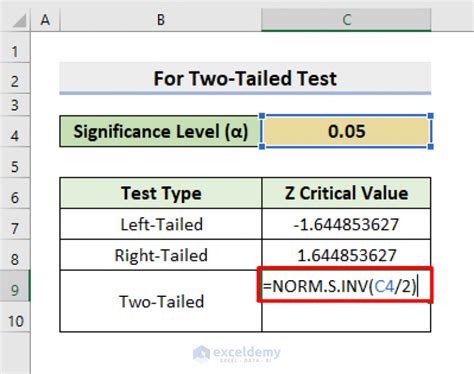
• Using the NORMINV Function: The NORMINV function in Excel returns the critical value from the standard normal distribution. The syntax for the NORMINV function is NORMINV(probability, mean, standard_deviation). For example, to find the critical value for a two-tailed test with a probability of 0.05, a mean of 0, and a standard deviation of 1, you would use the formula =NORMINV(0.05, 0, 1).
• Using the CRITBINOM Function: The CRITBINOM function in Excel returns the critical value from the binomial distribution. The syntax for the CRITBINOM function is CRITBINOM(trials, probability_s, alpha). For example, to find the critical value for a binomial test with 10 trials, a probability of success of 0.5, and an alpha of 0.05, you would use the formula =CRITBINOM(10, 0.5, 0.05).

Interpreting Critical Values

Once you have found the critical value, you can use it to determine whether to reject the null hypothesis. If the calculated test statistic is greater than the critical value, you reject the null hypothesis. If the calculated test statistic is less than the critical value, you fail to reject the null hypothesis.

Test Statistic	Critical Value	Decision
Greater than critical value		Reject null hypothesis
Less than critical value		Fail to reject null hypothesis

📝 Note: The critical value is a function of the sample size, the level of significance, and the type of test being performed.

Common Applications of Critical Values

Critical values have a wide range of applications in statistics, including:

• Hypothesis Testing: Critical values are used to determine whether a null hypothesis should be rejected or not.
• Confidence Intervals: Critical values are used to construct confidence intervals, which provide a range of values within which a population parameter is likely to lie.
• Regression Analysis: Critical values are used to determine the significance of regression coefficients.

In summary, finding critical values in Excel is an essential step in statistical analysis. By using the TINV, NORMINV, and CRITBINOM functions, you can easily find critical values and make informed decisions about your data.

To wrap things up, critical values play a vital role in statistical analysis, and understanding how to find and interpret them is crucial for making informed decisions about your data. By following the steps outlined in this post, you can easily find critical values in Excel and take your data analysis to the next level.