5 Ways Calculate Uncertainty

Introduction to Uncertainty Calculation
Calculating uncertainty is a crucial aspect of various fields, including science, engineering, and finance. Uncertainty refers to the degree of doubt or unpredictability associated with a measurement, prediction, or estimate. It is essential to quantify uncertainty to make informed decisions, assess risks, and allocate resources effectively. In this article, we will explore five ways to calculate uncertainty, highlighting the importance of each method and providing examples to illustrate their application.
1. Standard Deviation Method

The standard deviation method is a widely used approach to calculate uncertainty. It involves calculating the standard deviation of a dataset, which represents the average distance of each data point from the mean. The standard deviation (σ) is calculated using the following formula: σ = √[(Σ(xi - μ)²) / (n - 1)] where xi is each data point, μ is the mean, and n is the number of data points. The standard deviation method is useful for estimating uncertainty in datasets with a normal distribution.
2. Confidence Interval Method

The confidence interval method is another popular approach to calculate uncertainty. It involves constructing a range of values within which a population parameter is likely to lie. The confidence interval is calculated using the following formula: CI = x̄ ± (Z × (σ / √n)) where x̄ is the sample mean, Z is the Z-score corresponding to the desired confidence level, σ is the standard deviation, and n is the sample size. The confidence interval method provides a range of values within which the true population parameter is likely to lie, allowing for the estimation of uncertainty.
3. Monte Carlo Simulation Method

The Monte Carlo simulation method is a computational approach to calculate uncertainty. It involves running multiple simulations of a system or process, using random inputs to generate a range of possible outcomes. The Monte Carlo simulation method is useful for estimating uncertainty in complex systems, where analytical solutions are difficult to obtain. The method involves the following steps: * Define the system or process to be simulated * Generate random inputs for the simulation * Run multiple simulations to generate a range of possible outcomes * Analyze the results to estimate uncertainty
4. Bayesian Method
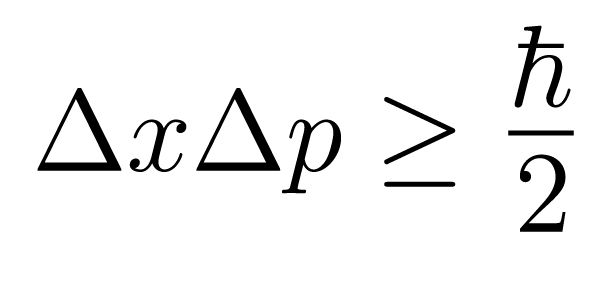
The Bayesian method is a statistical approach to calculate uncertainty, based on Bayes’ theorem. It involves updating the probability of a hypothesis based on new data or evidence. The Bayesian method is useful for estimating uncertainty in situations where there is prior knowledge or expertise. The method involves the following steps: * Define the prior distribution of the hypothesis * Update the prior distribution based on new data or evidence * Calculate the posterior distribution of the hypothesis * Estimate uncertainty using the posterior distribution
5. Fuzzy Logic Method

The fuzzy logic method is a mathematical approach to calculate uncertainty, based on fuzzy set theory. It involves representing uncertainty using fuzzy sets, which are sets with blurred boundaries. The fuzzy logic method is useful for estimating uncertainty in situations where there is ambiguity or vagueness. The method involves the following steps: * Define the fuzzy sets representing the uncertain variables * Calculate the membership functions of the fuzzy sets * Estimate uncertainty using the membership functions
💡 Note: The choice of method for calculating uncertainty depends on the specific problem or application, as well as the availability of data and computational resources.
Comparison of Methods

Each of the five methods for calculating uncertainty has its strengths and limitations. The standard deviation method is simple to implement but assumes a normal distribution of the data. The confidence interval method provides a range of values but requires a large sample size. The Monte Carlo simulation method is flexible but computationally intensive. The Bayesian method is useful for updating prior knowledge but requires a clear definition of the prior distribution. The fuzzy logic method is useful for representing ambiguity but requires a clear definition of the fuzzy sets.
| Method | Strengths | Limitations |
|---|---|---|
| Standard Deviation | Simple to implement | Assumes normal distribution |
| Confidence Interval | Provides range of values | Requires large sample size |
| Monte Carlo Simulation | Flexible and computationally intensive | Requires large computational resources |
| Bayesian | Updates prior knowledge | Requires clear definition of prior distribution |
| Fuzzy Logic | Represents ambiguity | Requires clear definition of fuzzy sets |

In summary, calculating uncertainty is a critical aspect of various fields, and there are several methods to estimate uncertainty, each with its strengths and limitations. By understanding the different methods and their applications, we can make informed decisions and allocate resources effectively.
What is uncertainty calculation?

+
Uncertainty calculation refers to the process of estimating the degree of doubt or unpredictability associated with a measurement, prediction, or estimate.
What are the different methods for calculating uncertainty?
+
The five methods for calculating uncertainty are: standard deviation method, confidence interval method, Monte Carlo simulation method, Bayesian method, and fuzzy logic method.
Which method is best for calculating uncertainty?
+
The choice of method for calculating uncertainty depends on the specific problem or application, as well as the availability of data and computational resources.