5 Ways Calculate P-Values

Introduction to P-Values
P-values are a crucial concept in statistical hypothesis testing, used to determine the significance of the results. In essence, a p-value measures the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. The calculation of p-values is fundamental in deciding whether to reject the null hypothesis or not. In this blog post, we will delve into the basics of p-values, their interpretation, and explore five ways to calculate p-values in different scenarios.
Understanding P-Values

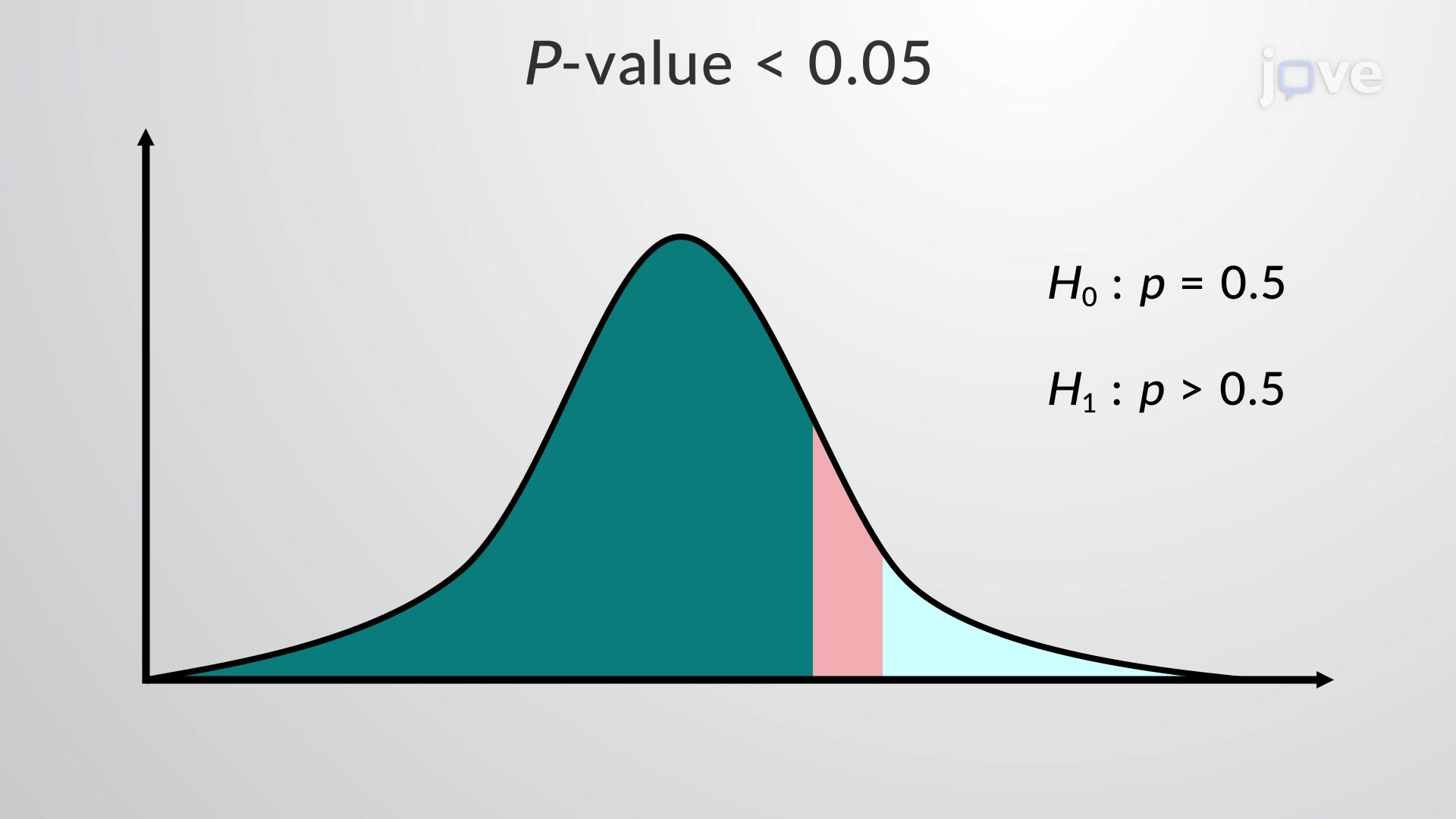
Before diving into the calculation methods, it’s essential to understand what p-values represent. A p-value is a numerical value that indicates whether the observed data would be highly unlikely under the null hypothesis. The lower the p-value, the stronger the evidence that the null hypothesis is not true. Typically, a p-value of less than 0.05 is considered statistically significant, leading to the rejection of the null hypothesis.
5 Ways to Calculate P-Values
Calculating p-values can be achieved through various methods, depending on the type of data and the hypothesis being tested. Here are five common ways to calculate p-values:
- Using Z-Scores: For large sample sizes, the z-score method can be employed to calculate p-values. This involves calculating the z-score of the observed value, then using a standard normal distribution table or calculator to find the corresponding p-value.
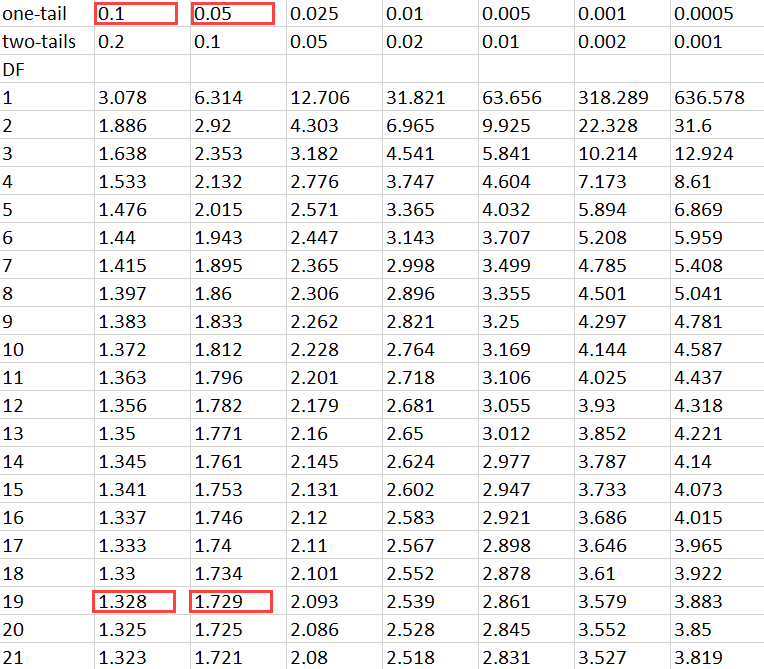
- Using T-Distribution: For smaller sample sizes, the t-distribution is used instead of the standard normal distribution. The t-score is calculated, and then the p-value is determined using a t-distribution table or calculator.
- Chi-Square Test: For categorical data, the chi-square test is commonly used to calculate p-values. This involves calculating the chi-square statistic, then using a chi-square distribution table or calculator to find the corresponding p-value.
- Non-Parametric Tests: For non-normal data or when the sample size is small, non-parametric tests such as the Wilcoxon rank-sum test or the Kruskal-Wallis test can be used to calculate p-values. These tests do not require any assumptions about the underlying distribution of the data.
- Simulation-Based Methods: In some cases, simulation-based methods such as bootstrapping or permutation tests can be used to calculate p-values. These methods involve simulating the data many times under the null hypothesis, then calculating the proportion of times the observed result or a more extreme result is obtained.
Interpretation of P-Values
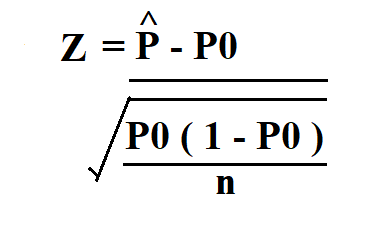
Once the p-value is calculated, it’s essential to interpret the result correctly. A small p-value (typically less than 0.05) indicates that the observed data would be highly unlikely under the null hypothesis, suggesting that the null hypothesis should be rejected. On the other hand, a large p-value indicates that the observed data are consistent with the null hypothesis, suggesting that the null hypothesis should not be rejected.
📝 Note: It's crucial to remember that p-values do not measure the probability of the null hypothesis being true or false but rather the probability of observing the data or more extreme data, assuming the null hypothesis is true.
Common Mistakes in P-Value Calculation
When calculating p-values, several common mistakes can be made, including: * Incorrectly assuming normality: Failing to check for normality of the data, leading to incorrect use of parametric tests. * Using the wrong test: Choosing a test that is not suitable for the type of data or hypothesis being tested. * Ignoring assumptions: Failing to check the assumptions of the test, such as independence or equal variances.
To avoid these mistakes, it’s essential to carefully evaluate the data and choose the correct test based on the research question and data characteristics.
Example Calculation of P-Value

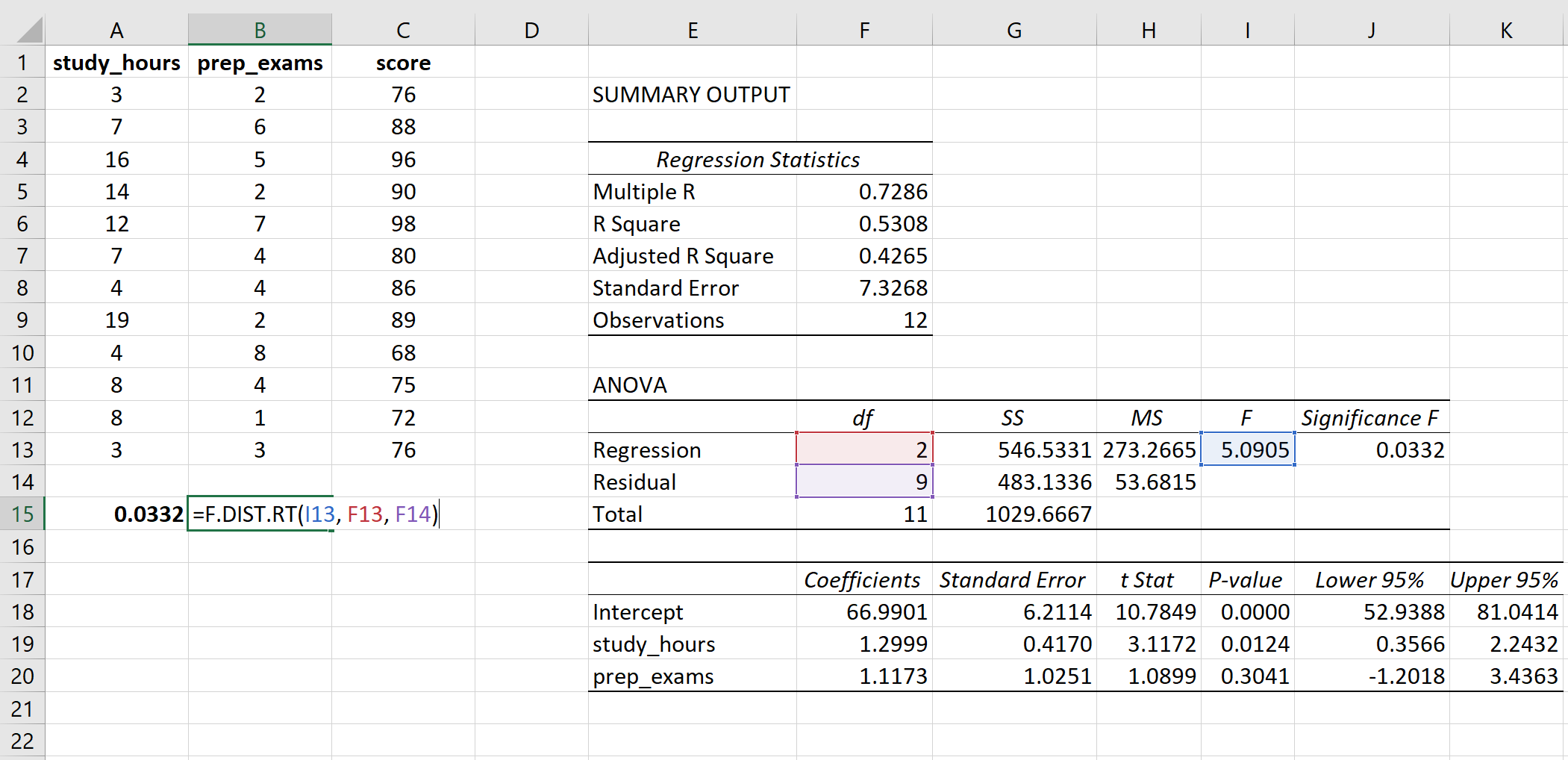
Let’s consider an example where we want to compare the means of two groups using a t-test. We calculate the t-score and then use a t-distribution table or calculator to find the corresponding p-value.
| Group | Mean | Standard Deviation | Sample Size |
|---|---|---|---|
| Group 1 | 10 | 2 | 20 |
| Group 2 | 12 | 3 | 25 |
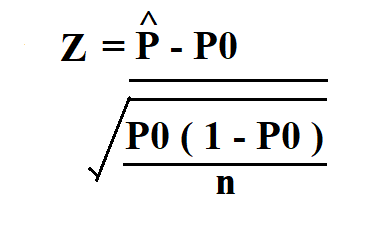
Using a t-test calculator, we find that the t-score is 2.5, and the corresponding p-value is 0.01. Since the p-value is less than 0.05, we reject the null hypothesis, suggesting that the means of the two groups are statistically significantly different.
In summary, calculating p-values is a critical step in statistical hypothesis testing. By understanding the different methods of calculating p-values and interpreting the results correctly, researchers can make informed decisions about their data and hypotheses.
What is the purpose of calculating p-values?
+
The purpose of calculating p-values is to determine the statistical significance of the results, which helps in making informed decisions about the null hypothesis.
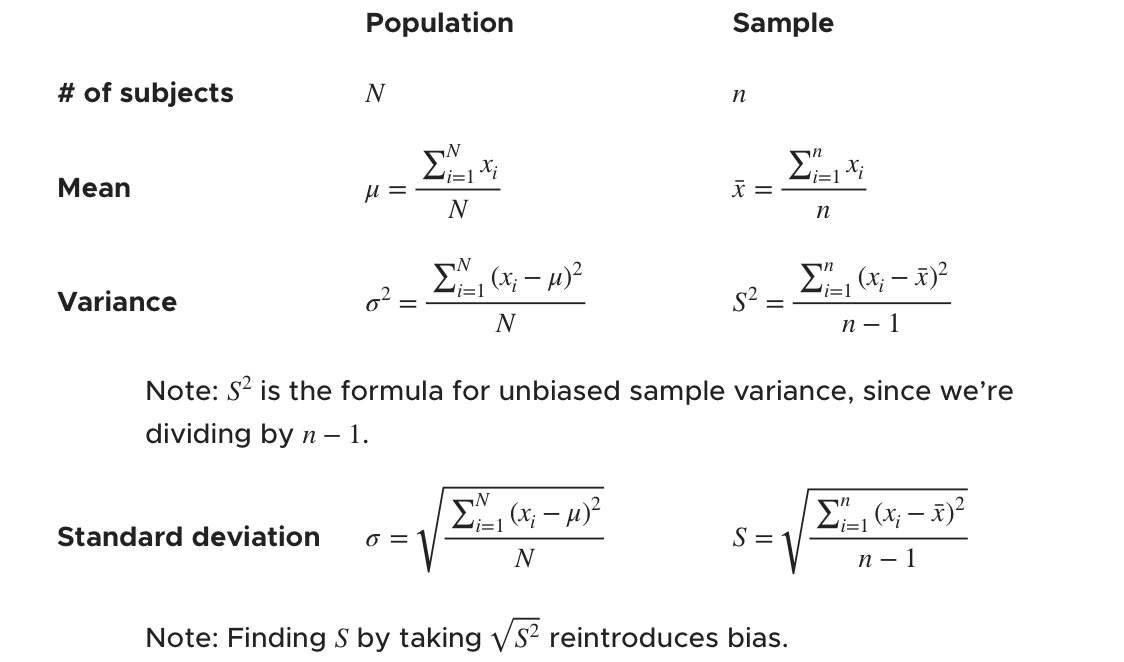
What is the difference between a z-score and a t-score?
+
A z-score is used for large sample sizes and is calculated using the standard normal distribution, whereas a t-score is used for smaller sample sizes and is calculated using the t-distribution.
What are the common mistakes made when calculating p-values?
+
Common mistakes include incorrectly assuming normality, using the wrong test, and ignoring assumptions such as independence or equal variances.