5 Ways To Calculate P-Value
Understanding P-Value
The p-value, or probability value, is a key concept in statistical hypothesis testing, representing the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. It is a crucial metric for determining the significance of the results obtained from a statistical test. The calculation of the p-value varies depending on the type of test being conducted. Here, we will explore five common methods for calculating the p-value, each applicable to different types of data and hypotheses.
1. Using the Z-Test for Large Samples

For large samples, the Z-test is commonly used to calculate the p-value. This method assumes that the sample size is sufficiently large (usually n > 30) and that the population standard deviation is known. The formula for the Z-score is: [ Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} ] where (\bar{X}) is the sample mean, (\mu) is the population mean under the null hypothesis, (\sigma) is the population standard deviation, and (n) is the sample size. The p-value can then be found by looking up the Z-score in a standard normal distribution table or by using statistical software.
2. Applying the T-Test for Small Samples
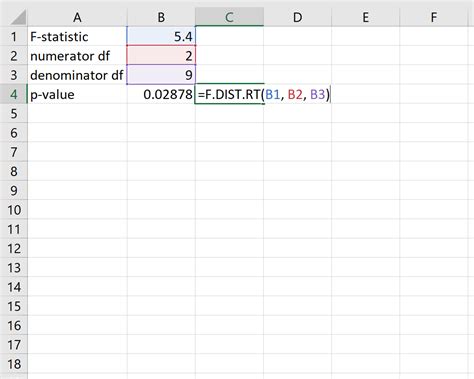
When dealing with small samples (n ≤ 30) and the population standard deviation is unknown, the T-test is the appropriate method. The T-score formula is: [ T = \frac{\bar{X} - \mu}{s / \sqrt{n}} ] where (s) is the sample standard deviation. The p-value is determined by referring to a t-distribution table with the appropriate degrees of freedom (n-1) or by using statistical software.
3. Chi-Square Test for Categorical Data

The Chi-Square test is used for categorical data to determine if there is a significant association between two variables. The formula for the Chi-Square statistic is: [ \chi^2 = \sum \frac{(Observed - Expected)^2}{Expected} ] The p-value is found by looking up the Chi-Square statistic in a Chi-Square distribution table with the appropriate degrees of freedom or by using statistical software.
4. ANOVA for Comparing Multiple Means
Analysis of Variance (ANOVA) is used to compare means among three or more groups. The F-statistic is calculated as: [ F = \frac{MS{between}}{MS{within}} ] where (MS{between}) is the mean square between groups, and (MS{within}) is the mean square within groups. The p-value is determined by referring to an F-distribution table with the appropriate degrees of freedom or by using statistical software.
5. Non-Parametric Tests for Non-Normal Data
For data that does not meet the assumptions of normality or equal variances, non-parametric tests are used. An example is the Wilcoxon rank-sum test for comparing two independent groups. The test statistic is calculated based on the ranks of the data, and the p-value is often determined using statistical software due to the complexity of the calculations.
📝 Note: The choice of method for calculating the p-value depends on the nature of the data, the type of hypothesis being tested, and whether the data meet the assumptions required for parametric tests.
In practice, calculating the p-value involves understanding the research question, selecting the appropriate statistical test, and interpreting the results in the context of the study. It is crucial to ensure that the assumptions of the chosen test are met to avoid misleading conclusions. With the advancement of statistical software, the actual calculation of p-values has become more accessible, allowing researchers to focus on the interpretation and implications of their findings.
To summarize the key points: - The p-value calculation method depends on the type of data and the hypothesis being tested. - Common methods include the Z-test, T-test, Chi-Square test, ANOVA, and non-parametric tests. - Understanding the assumptions of each test and ensuring they are met is vital for valid results. - The interpretation of the p-value should be done with caution, considering the context of the study and the potential for Type I or Type II errors.
The process of calculating and interpreting p-values is fundamental to statistical analysis, providing a quantitative measure of the strength of evidence against a null hypothesis. By selecting the appropriate method and correctly interpreting the results, researchers can draw meaningful conclusions from their data.
What is the primary purpose of calculating the p-value in statistical testing?

+
The primary purpose of calculating the p-value is to determine the significance of the results obtained from a statistical test, indicating the probability of observing the results (or more extreme) assuming that the null hypothesis is true.
How do you choose the appropriate method for calculating the p-value?
+
The choice of method depends on the nature of the data (continuous, categorical), the size of the sample, whether the data meet the assumptions of normality and equal variances, and the type of hypothesis being tested (one-tailed, two-tailed).
What are the common misconceptions about p-values that researchers should be aware of?
+
Common misconceptions include misunderstanding the p-value as the probability that the null hypothesis is true, ignoring the context and assumptions of the test, and not considering the potential for Type I or Type II errors. It’s also important to remember that a significant p-value does not necessarily imply practical significance.