5 Ways To Find Z-Score
Introduction to Z-Score
The Z-score, also known as the standard score, is a statistical measure that describes a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean. If a value has a Z-score of 0, it is equal to the mean. A Z-score of 1 means the value is 1 standard deviation from the mean, and so on. The Z-score is an important concept in statistics, and it is used in a variety of applications, including hypothesis testing, confidence intervals, and prediction intervals. In this article, we will discuss 5 ways to find the Z-score.
Understanding the Formula

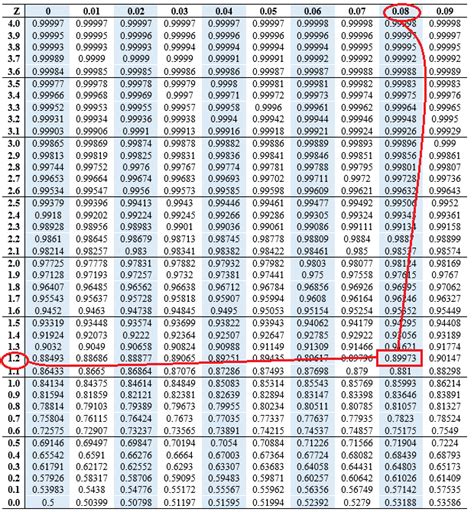
Before we dive into the methods of finding the Z-score, let’s first understand the formula. The Z-score formula is given by: Z = (X - μ) / σ where: - Z is the Z-score - X is the value of the element - μ is the mean of the dataset - σ is the standard deviation of the dataset The Z-score can be positive or negative. A positive Z-score indicates that the value is above the mean, while a negative Z-score indicates that the value is below the mean.
Method 1: Using a Z-Score Calculator
One of the easiest ways to find the Z-score is by using a Z-score calculator. There are many online calculators available that can calculate the Z-score for you. All you need to do is enter the value, mean, and standard deviation, and the calculator will give you the Z-score. This method is quick and easy, but it may not be suitable for everyone, especially those who want to understand the underlying mathematics.
Method 2: Using a Statistical Software
Another way to find the Z-score is by using statistical software such as R or Python. These software programs have built-in functions that can calculate the Z-score for you. For example, in R, you can use the scale() function to calculate the Z-score. In Python, you can use the scipy.stats.zscore() function. This method is suitable for those who are familiar with programming and want to perform more complex statistical analysis.
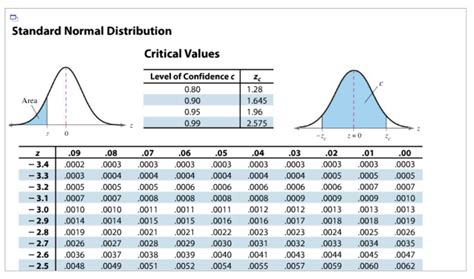
Method 3: Using a Z-Score Table
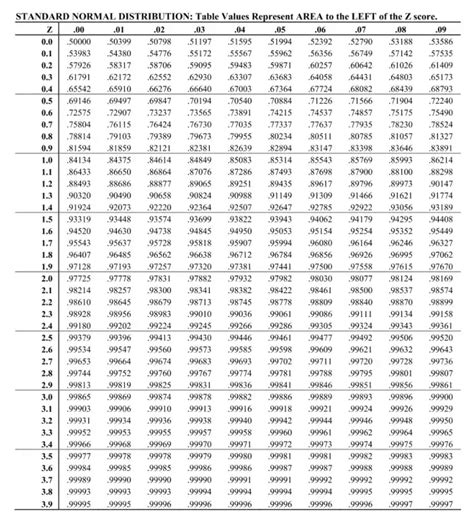
A Z-score table, also known as a standard normal distribution table, is a table that shows the probability of a value being less than or equal to a given Z-score. The table can be used to find the Z-score for a given value, mean, and standard deviation. To use the table, you need to first calculate the Z-score using the formula, and then look up the corresponding probability in the table. This method is suitable for those who want to understand the underlying mathematics and do not have access to a calculator or computer.
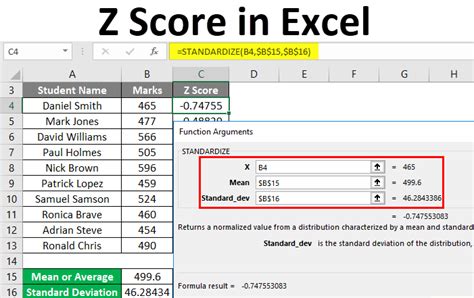
Method 4: Using a Spreadsheet

You can also use a spreadsheet program such as Microsoft Excel to calculate the Z-score. The formula for calculating the Z-score can be entered into a cell, and the Z-score will be calculated automatically. This method is suitable for those who are familiar with spreadsheets and want to perform more complex statistical analysis.
Method 5: Manual Calculation
Finally, you can also calculate the Z-score manually using the formula. This method is suitable for those who want to understand the underlying mathematics and do not have access to a calculator or computer. To calculate the Z-score manually, you need to first calculate the mean and standard deviation of the dataset, and then use the formula to calculate the Z-score.
📝 Note: Manual calculation of the Z-score can be time-consuming and prone to errors, especially for large datasets. It is recommended to use a calculator or computer program to calculate the Z-score whenever possible.
Here is a table summarizing the 5 methods of finding the Z-score:
| Method | Description |
|---|---|
| 1. Using a Z-Score Calculator | Quick and easy, but may not be suitable for everyone |
| 2. Using a Statistical Software | Suitable for those who are familiar with programming and want to perform more complex statistical analysis |
| 3. Using a Z-Score Table | Suitable for those who want to understand the underlying mathematics and do not have access to a calculator or computer |
| 4. Using a Spreadsheet | Suitable for those who are familiar with spreadsheets and want to perform more complex statistical analysis |
| 5. Manual Calculation | Suitable for those who want to understand the underlying mathematics and do not have access to a calculator or computer, but can be time-consuming and prone to errors |
In summary, there are 5 ways to find the Z-score: using a Z-score calculator, using a statistical software, using a Z-score table, using a spreadsheet, and manual calculation. Each method has its own advantages and disadvantages, and the choice of method depends on the individual’s needs and preferences. The Z-score is an important concept in statistics, and understanding how to calculate it is essential for anyone who wants to work with data.
What is the Z-score formula?

+
The Z-score formula is given by: Z = (X - μ) / σ, where Z is the Z-score, X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation of the dataset.
What is the difference between a positive and negative Z-score?

+
A positive Z-score indicates that the value is above the mean, while a negative Z-score indicates that the value is below the mean.
Can I calculate the Z-score manually?

+
Yes, you can calculate the Z-score manually using the formula. However, it is recommended to use a calculator or computer program to calculate the Z-score whenever possible, as manual calculation can be time-consuming and prone to errors.
What is the purpose of the Z-score?
+
The Z-score is used to describe a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean, and it is used in a variety of applications, including hypothesis testing, confidence intervals, and prediction intervals.
Can I use a spreadsheet to calculate the Z-score?

+
Yes, you can use a spreadsheet program such as Microsoft Excel to calculate the Z-score. The formula for calculating the Z-score can be entered into a cell, and the Z-score will be calculated automatically.