5 Ways Calculate Slope
Introduction to Slope Calculation
Calculating the slope of a line is a fundamental concept in mathematics and is used in various fields such as physics, engineering, and geography. The slope of a line represents how steep it is and can be calculated using different methods. In this article, we will explore five ways to calculate the slope of a line.
Method 1: Using the Slope Formula

The most common method to calculate the slope of a line is by using the slope formula: m = (y2 - y1) / (x2 - x1), where m is the slope, and (x1, y1) and (x2, y2) are two points on the line. This formula is widely used and is a straightforward way to calculate the slope.
Method 2: Using the Graph of a Line
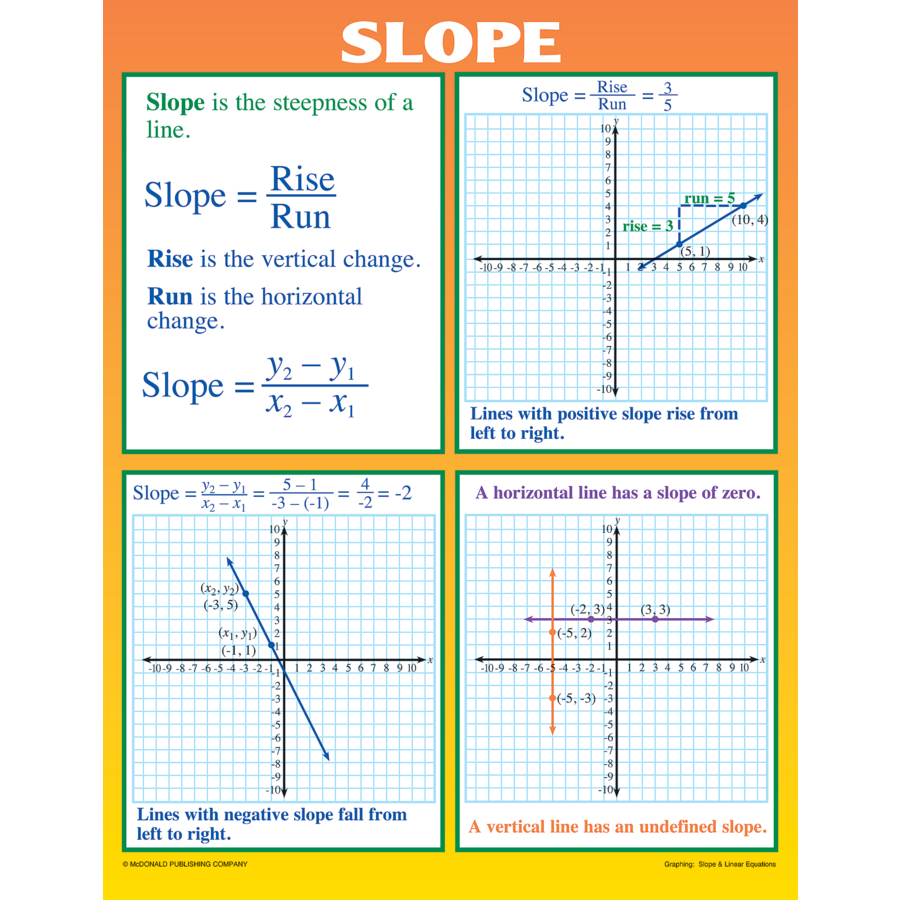
Another way to calculate the slope of a line is by using its graph. By plotting two points on the line, we can calculate the rise and run of the line, which can then be used to calculate the slope. The rise is the vertical distance between the two points, and the run is the horizontal distance. The slope can be calculated using the formula: m = rise / run.
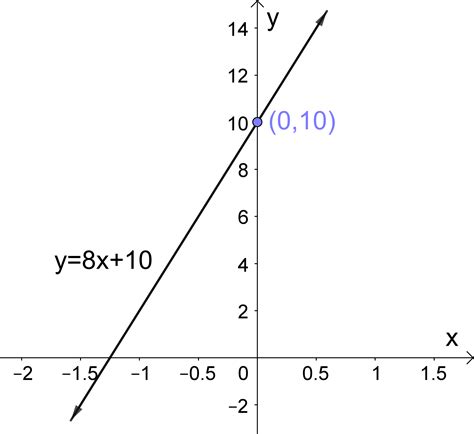
Method 3: Using the Equation of a Line
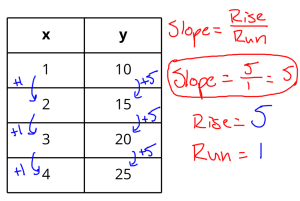
If we have the equation of a line in the form y = mx + b, where m is the slope and b is the y-intercept, we can directly read the slope from the equation. This method is useful when we already have the equation of the line and need to find its slope.
Method 4: Using the Angle of Elevation
The slope of a line can also be calculated using the angle of elevation, which is the angle between the line and the horizontal. The slope can be calculated using the formula: m = tan(θ), where θ is the angle of elevation. This method is useful when we know the angle of elevation and need to find the slope.
Method 5: Using a Calculator or Computer Program
Finally, we can use a calculator or computer program to calculate the slope of a line. Many calculators and computer programs have built-in functions to calculate the slope of a line given two points or the equation of the line. This method is useful when we need to calculate the slope quickly and accurately.
📝 Note: When calculating the slope of a line, it is essential to ensure that the units of the rise and run are the same, as this can affect the accuracy of the calculation.
Some key points to consider when calculating the slope of a line include: * Ensuring that the units of the rise and run are the same * Using the correct formula for the given method * Double-checking calculations for accuracy * Considering the context in which the slope is being used
| Method | Formula | Description |
|---|---|---|
| Slope Formula | m = (y2 - y1) / (x2 - x1) | Uses two points on the line to calculate the slope |
| Graph of a Line | m = rise / run | Uses the graph of the line to calculate the slope |
| Equation of a Line | y = mx + b | Uses the equation of the line to calculate the slope |
| Angle of Elevation | m = tan(θ) | Uses the angle of elevation to calculate the slope |
| Calculator or Computer Program | Varies | Uses a calculator or computer program to calculate the slope |

In summary, there are several ways to calculate the slope of a line, each with its own advantages and disadvantages. By understanding these different methods, we can choose the most appropriate one for a given situation and ensure accurate calculations. The ability to calculate the slope of a line is a fundamental skill that has numerous applications in various fields, and mastering it can lead to a deeper understanding of mathematical concepts and their practical applications.
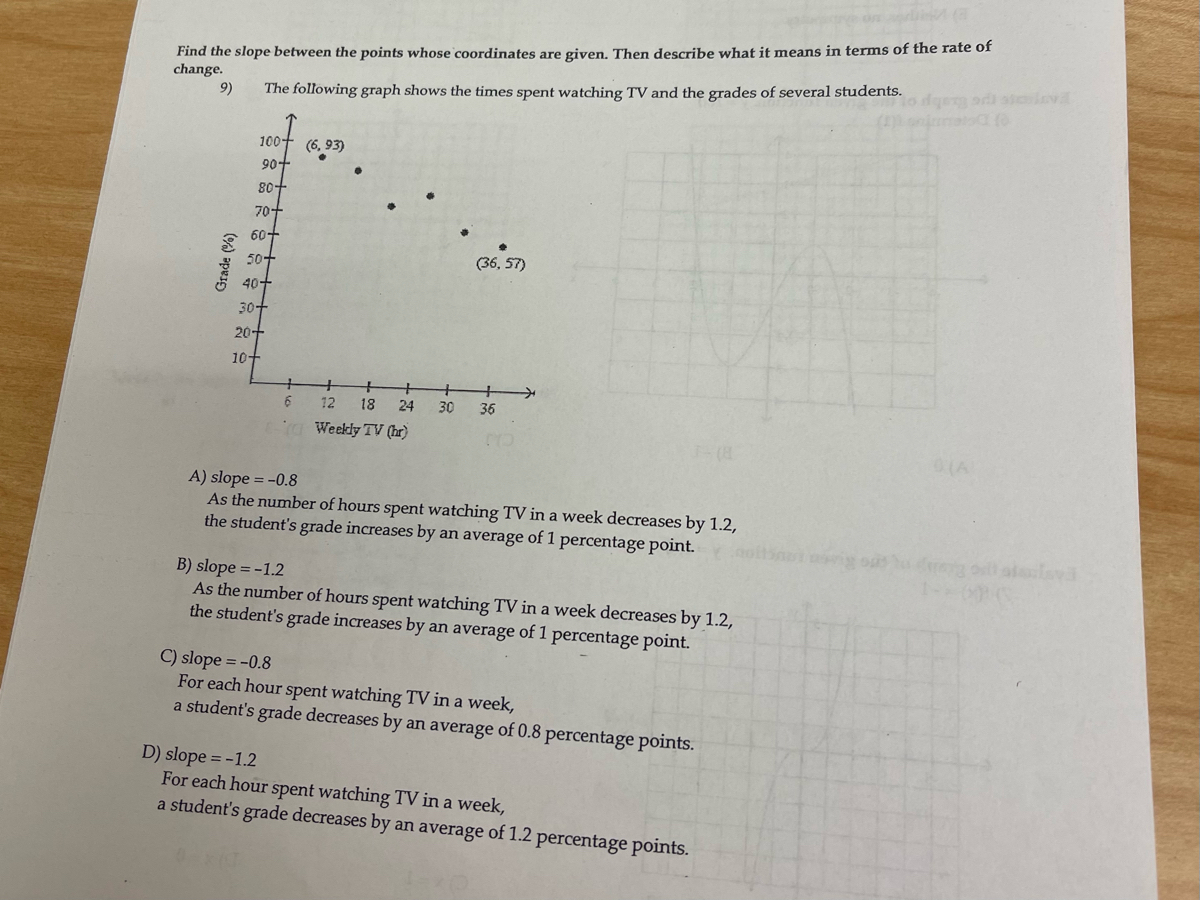
What is the slope of a line?
+
The slope of a line represents how steep it is and can be calculated using different methods, including the slope formula, the graph of a line, the equation of a line, the angle of elevation, and a calculator or computer program.
What is the slope formula?

+
The slope formula is m = (y2 - y1) / (x2 - x1), where m is the slope, and (x1, y1) and (x2, y2) are two points on the line.
How do I calculate the slope of a line using the graph?

+
To calculate the slope of a line using the graph, plot two points on the line, calculate the rise (vertical distance) and run (horizontal distance), and then use the formula m = rise / run.



