5 Ways Square Root

Introduction to Square Roots
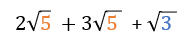
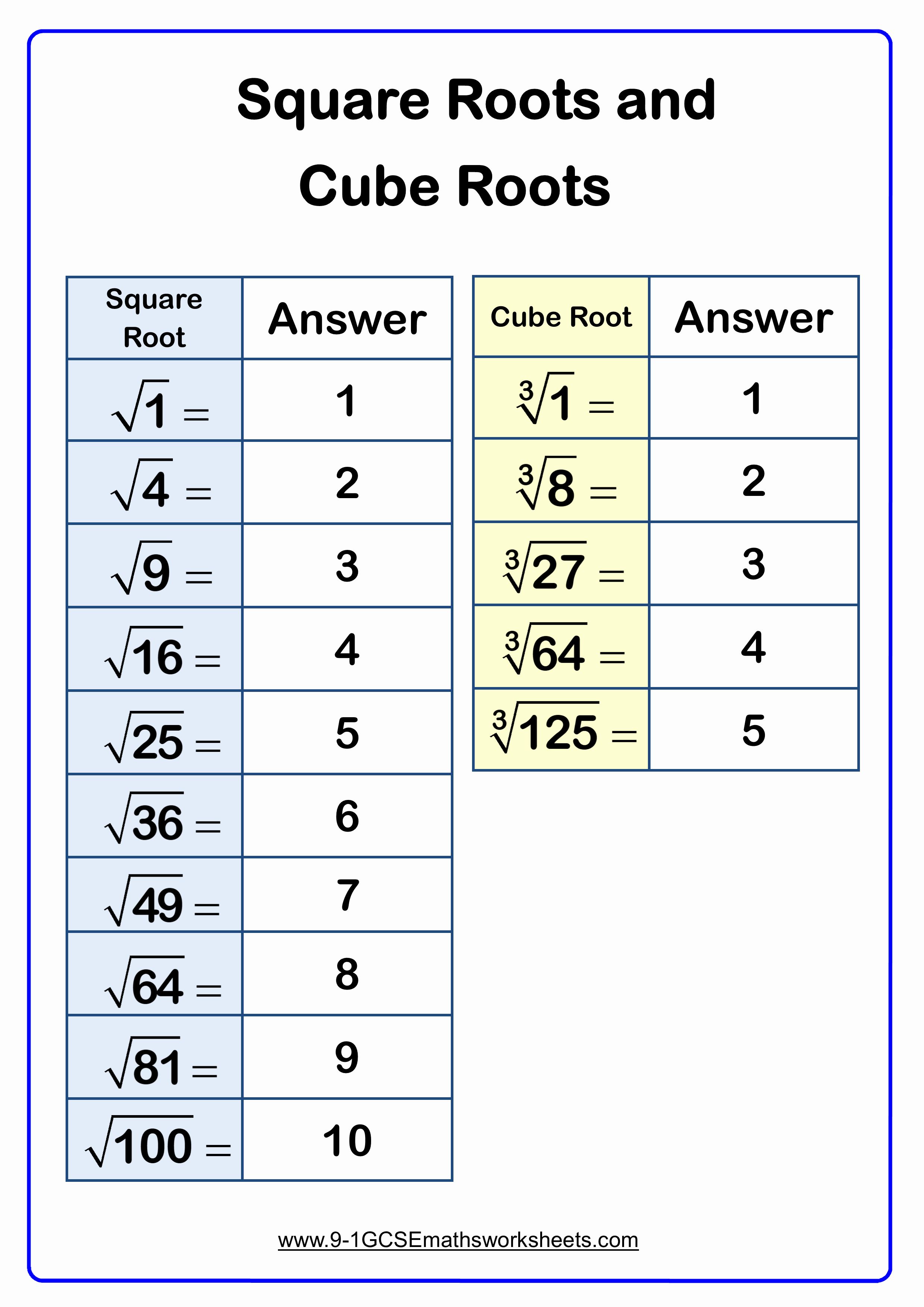
The concept of square roots is fundamental in mathematics, particularly in algebra and geometry. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 16 is 4 because 4 multiplied by 4 equals 16. The symbol for square root is √, and it is used in various mathematical operations, including solving equations and calculating distances. In this article, we will explore five ways to calculate square roots, highlighting their importance and applications in different fields.
Method 1: Using a Calculator

One of the simplest and most straightforward methods to find the square root of a number is by using a calculator. Most calculators have a dedicated square root button, often denoted by the √ symbol. To find the square root of a number, simply enter the number into the calculator and press the square root button. This method is quick and accurate, making it a favorite among students and professionals alike. However, it’s essential to understand the mathematical concept behind square roots, as relying solely on calculators can hinder the development of problem-solving skills.
Method 2: Long Division Method
The long division method is a manual way to calculate square roots. It involves dividing the number for which you want to find the square root (the dividend) by a series of perfect squares, progressively narrowing down the options until you reach the closest approximation of the square root. This method requires a good understanding of perfect squares and can be time-consuming, but it provides a hands-on approach to calculating square roots without a calculator.
Method 3: Prime Factorization

Another method to find the square root of a number is through prime factorization. This involves breaking down the number into its prime factors and then grouping these factors in pairs of the same number. The product of each pair represents a perfect square, and the square root of the number can be determined by taking the square root of each perfect square factor. For example, to find the square root of 36, you break it down into its prime factors: 36 = 2 * 2 * 3 * 3. Grouping these into pairs gives (2*2) * (3*3), which simplifies to 6 * 6, and thus the square root of 36 is 6.
Method 4: Using Algebraic Identities

Algebraic identities can also be used to simplify expressions involving square roots. For instance, the identity (a+b)^2 = a^2 + 2ab + b^2 can be used to expand and simplify square root expressions. Additionally, identities like (a-b)^2 = a^2 - 2ab + b^2 can help in factorizing expressions and finding square roots. This method is particularly useful in solving quadratic equations and other algebraic problems.
Method 5: Approximation Techniques
For very large numbers or when a precise calculation is not necessary, approximation techniques can be used to estimate the square root. One common method is the Babylonian method, which involves making an initial guess and then iteratively improving the guess using a formula until the desired level of accuracy is reached. Another method is to use the fact that the square root of a number lies between two consecutive perfect squares. For example, since 16 < 20 < 25, the square root of 20 must lie between 4 and 5. This can provide a quick and rough estimate of the square root without the need for precise calculations.
📝 Note: Understanding and being able to apply these different methods for calculating square roots can greatly enhance problem-solving skills and flexibility in mathematical and real-world applications.
In summary, calculating square roots is a fundamental skill in mathematics that can be approached in various ways, each with its advantages and applications. Whether using a calculator for quick results, applying manual methods like long division or prime factorization for a deeper understanding, utilizing algebraic identities for simplification, or employing approximation techniques for estimates, mastering these methods can significantly improve one’s proficiency in mathematics and related fields. The ability to calculate square roots efficiently and accurately is essential for advancing in mathematics and applying mathematical concepts to real-world problems.