Get P Value From T Test In Excel
Introduction to T-Test and P-Value in Excel
When analyzing data in Excel, statistical tests like the T-Test are crucial for understanding the significance of differences between groups. One key outcome of the T-Test is the P-Value, which helps determine whether the observed differences are due to chance or if they are statistically significant. In this article, we will explore how to perform a T-Test in Excel and how to interpret the P-Value.
Understanding T-Test and P-Value

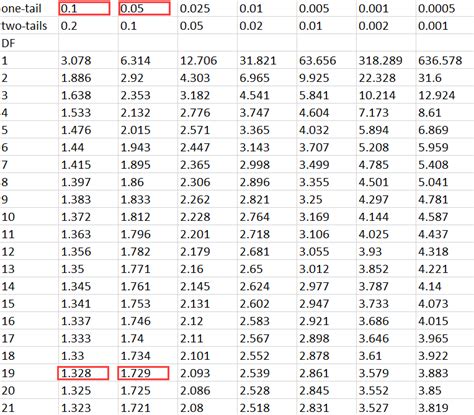
The T-Test is a statistical method used to compare the means of two groups to see if there is a significant difference between them. The test can be one-tailed (testing for a difference in one direction) or two-tailed (testing for a difference in either direction). The P-Value, or probability value, is a key component of the T-Test. It represents the probability of observing the results of the test (or more extreme) if the null hypothesis is true. The null hypothesis typically states that there is no significant difference between the means of the two groups.
Performing a T-Test in Excel

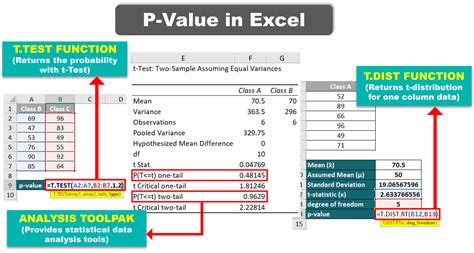
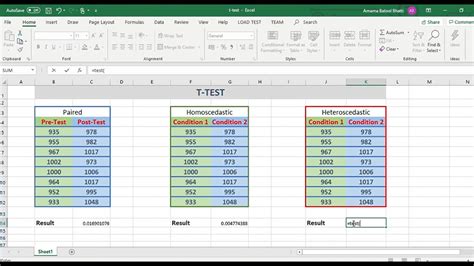
To perform a T-Test in Excel, you can use the built-in function
T.TEST or the Analysis ToolPak add-in. Here, we’ll focus on using the T.TEST function because it’s more straightforward and doesn’t require additional setup.
- Prepare Your Data: Ensure your data is organized into two columns, each representing the group you want to compare.
- Use the T.TEST Function:
- The syntax for the
T.TESTfunction isT.TEST(array1, array2, tails, type). array1andarray2are the ranges of the two groups of data.tailsspecifies the number of tails for the test: 1 for a one-tailed test or 2 for a two-tailed test.typespecifies the type of T-Test: 1 for a paired test, 2 for a two-sample test with equal variances, or 3 for a two-sample test with unequal variances.- Example: If you have data in columns A and B, and you want to perform a two-tailed, two-sample test with unequal variances, the formula would be
=T.TEST(A1:A10, B1:B10, 2, 3).
- The syntax for the
Interpreting the P-Value

After performing the T-Test, you’ll get a P-Value. The interpretation of this value is crucial: - If the P-Value is less than your chosen significance level (commonly 0.05), you reject the null hypothesis. This means there is a statistically significant difference between the means of the two groups. - If the P-Value is greater than your chosen significance level, you fail to reject the null hypothesis, suggesting that the observed differences between the means could be due to chance.
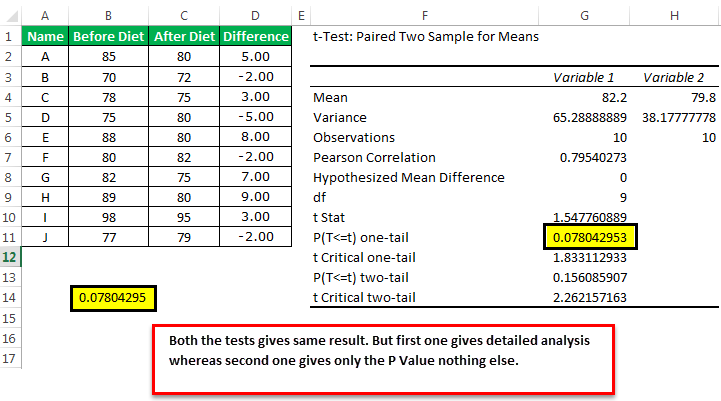
Example Walkthrough
Let’s say we have two groups of students, and we want to see if there’s a significant difference in their average scores on a particular test.
| Group A | Group B |
|---|---|
| 85 | 80 |
| 90 | 85 |
| 78 | 82 |
| … | … |

To perform a two-tailed, two-sample T-Test with unequal variances:
1. Select a cell where you want the result to appear.
2. Type =T.TEST(A1:A20, B1:B20, 2, 3), assuming your data ranges from A1 to A20 for Group A and B1 to B20 for Group B.
3. Press Enter to get the P-Value.
If the P-Value returned is 0.01, and considering a significance level of 0.05, you would conclude that there is a statistically significant difference between the average scores of the two groups.
📝 Note: Always ensure your data meets the assumptions of the T-Test, including normality of the data and equality of variances for certain types of T-Tests.
Best Practices and Considerations
- Data Normality: Ensure that your data is normally distributed, as the T-Test assumes normality. - Sample Size: Larger sample sizes provide more reliable results. - Significance Level: Choose an appropriate significance level based on your research question and the acceptable risk of Type I error.
Using Analysis ToolPak for T-Test

If you prefer a more guided approach or need additional statistical tests, the Analysis ToolPak add-in can be useful. To access it, go to the “Data” tab in Excel, click “Data Analysis,” and then select “t-Test: Two-Sample Assuming Unequal Variances” or the appropriate test for your data.
Conclusion and Final Thoughts

Understanding and interpreting the P-Value from a T-Test in Excel is a fundamental skill for data analysis. By following the steps outlined and considering the assumptions and limitations of the T-Test, you can make informed decisions based on your data. Remember, the P-Value is a measure of the strength of evidence against a null hypothesis, and its interpretation should be done with care, considering the context and potential implications of your findings.
What is the main purpose of the T-Test in data analysis?
+
The main purpose of the T-Test is to determine if there is a significant difference between the means of two groups.
How do I choose the right type of T-Test for my data?

+
The choice of T-Test depends on whether your data is paired or unpaired and whether the variances of the two groups are equal or unequal. You also need to decide if you’re performing a one-tailed or two-tailed test based on your hypothesis.
What does a P-Value of 0.05 indicate in the context of a T-Test?

+
A P-Value of 0.05 indicates that if the null hypothesis is true, the probability of observing the results you have (or more extreme) is 5%. This is commonly used as a threshold for significance, meaning if your P-Value is less than or equal to 0.05, you reject the null hypothesis and conclude there is a statistically significant difference.