Find P Value In Excel Easily

Introduction to P-Value in Statistical Analysis

In statistical analysis, the p-value, or probability value, is a key concept that helps researchers determine the significance of their findings. It measures the strength of evidence against a null hypothesis, indicating whether the observed data could have occurred by chance. In this article, we will explore how to find the p-value in Excel easily, making statistical analysis more accessible to a broader audience.

Understanding P-Value

Before diving into the process of calculating the p-value in Excel, it’s essential to understand what it represents. The p-value is a number between 0 and 1 that indicates the probability of observing the results of your study, or more extreme, if the null hypothesis is true. A small p-value (typically less than 0.05) suggests that the observed data would be very unlikely under the null hypothesis, leading to the rejection of the null hypothesis and the conclusion that the results are statistically significant.

Calculating P-Value in Excel

Excel provides several functions to calculate the p-value for different types of statistical tests. Here are the steps for some common scenarios:

• For a Two-Tailed T-Test:

  1. Enter your data into two columns in Excel.
  2. Go to the “Data” tab and click on “Data Analysis” in the “Analysis” group. If you don’t see “Data Analysis,” you might need to install the Analysis ToolPak add-in.
  3. Select “t-Test: Two-Sample Assuming Equal Variances” (or “t-Test: Two-Sample Assuming Unequal Variances” depending on your data) and click “OK.”
  4. Input the range for your two datasets, select the appropriate options, and click “OK.”
  5. Excel will output the results, including the p-value.

• For a One-Tailed T-Test or Other Tests: You can use the T.TEST function in Excel for one-tailed tests or for more specific scenarios. The syntax is T.TEST(array1, array2, tails, type), where:

  • array1 and array2 are the ranges of the two datasets.
  • tails specifies whether the test is one-tailed (1) or two-tailed (2).
  • type specifies the type of t-test (1 for paired, 2 for two-sample equal variance, 3 for two-sample unequal variance).

Using Excel Functions for P-Value Calculation

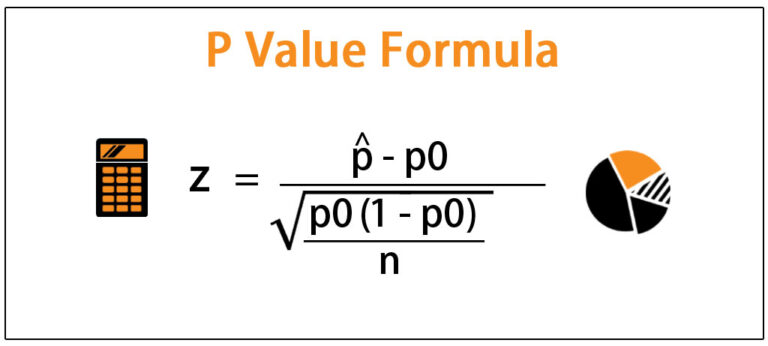
Excel offers several built-in functions for calculating p-values directly, depending on the type of statistical test you are performing. For instance: - CHISQ.TEST for chi-square tests of independence. - F.TEST for F-tests, which are used in analysis of variance (ANOVA). - Z.TEST for z-tests, which compare the mean of a sample to a known population mean.

These functions simplify the process of finding p-values without needing to navigate through menus or add-ins.

Interpreting P-Values

Once you have calculated the p-value, the next step is to interpret it. Here are some guidelines: - If the p-value is less than your chosen significance level (usually 0.05), you reject the null hypothesis, suggesting that the observed effect is statistically significant. - If the p-value is greater than your chosen significance level, you fail to reject the null hypothesis, indicating that the observed effect might be due to chance.

It’s crucial to understand that a small p-value does not necessarily imply a large or practically significant effect. It only indicates that the observed effect is unlikely to occur by chance if the null hypothesis is true.

Common Mistakes in Interpreting P-Values

There are several common misconceptions about p-values that can lead to incorrect interpretations: - Mistaking statistical significance for practical significance. A result can be statistically significant without being practically significant or meaningful. - Believing that the p-value measures the probability that the null hypothesis is true. It actually measures the probability of observing the results (or more extreme) assuming the null hypothesis is true. - Overlooking the impact of sample size. Larger samples can detect smaller effects, potentially leading to statistically significant results that are not practically significant.

📝 Note: Always consider the context, sample size, and the actual difference or effect size when interpreting p-values, rather than relying solely on the statistical significance.

To summarize the key points about finding and interpreting p-values in Excel: - Use built-in functions like T.TEST, CHISQ.TEST, F.TEST, and Z.TEST for direct calculations. - Interpret the p-value in the context of your research question and significance level. - Avoid common pitfalls in interpretation, such as confusing statistical significance with practical significance.

The ability to easily calculate and interpret p-values in Excel enhances the analytical capabilities of researchers and analysts, making statistical decision-making more accessible and informed.

Finding the p-value is a crucial step in statistical analysis that helps in determining the significance of the results. By following the steps outlined above and using the appropriate Excel functions, you can easily calculate the p-value for various statistical tests. Remember, the p-value is just one part of the analysis; consider it in conjunction with effect sizes, confidence intervals, and practical significance to draw meaningful conclusions from your data.