5 Ways To Calculate Average Percentage
Introduction to Average Percentage Calculations
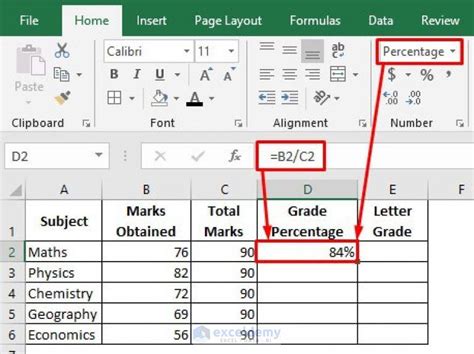
Calculating the average percentage is a crucial task in various fields, including finance, education, and statistics. It helps in understanding the overall performance, growth rate, or success rate of a particular entity or group. In this article, we will explore five different methods to calculate the average percentage, along with their formulas, examples, and applications.
Method 1: Simple Average Percentage
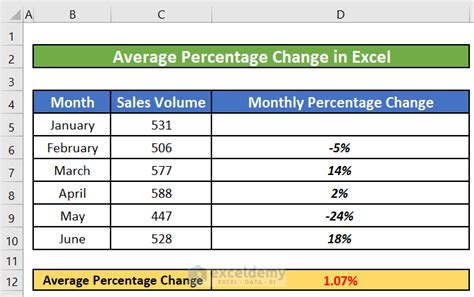
The simple average percentage is calculated by adding up all the percentages and then dividing by the total number of values. The formula for this method is: Simple Average Percentage = (Sum of all percentages) / (Total number of values) For example, if we want to calculate the average percentage of marks scored by a student in five subjects, we can use this method.
Method 2: Weighted Average Percentage
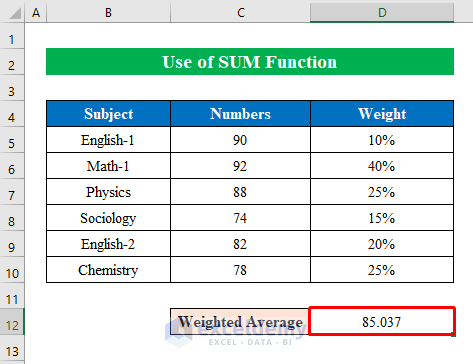
The weighted average percentage is used when each percentage has a different weight or importance. The formula for this method is: Weighted Average Percentage = (Sum of (percentage x weight)) / (Sum of weights) This method is useful in scenarios where some percentages have a greater impact than others.
Method 3: Geometric Average Percentage
The geometric average percentage is used to calculate the average growth rate of a quantity over a period. The formula for this method is: Geometric Average Percentage = (Product of (1 + percentage))^(1/n) - 1 where n is the number of periods. This method is commonly used in finance to calculate the average return on investment.
Method 4: Harmonic Average Percentage

The harmonic average percentage is used to calculate the average rate of a quantity over a period. The formula for this method is: Harmonic Average Percentage = n / (Sum of (1/percentage)) where n is the number of periods. This method is useful in scenarios where the rates are not constant over time.
Method 5: Median Average Percentage
The median average percentage is used to calculate the middle value of a set of percentages. The formula for this method is: Median Average Percentage = Middle value of the ordered set of percentages This method is useful in scenarios where the set of percentages is not normally distributed.
📝 Note: The choice of method depends on the specific application and the characteristics of the data.
The following table summarizes the five methods:
| Method | Formula | Application |
|---|---|---|
| Simple Average Percentage | (Sum of all percentages) / (Total number of values) | General calculations |
| Weighted Average Percentage | (Sum of (percentage x weight)) / (Sum of weights) | Scenarios with different weights |
| Geometric Average Percentage | (Product of (1 + percentage))^(1/n) - 1 | Finance and growth rate calculations |
| Harmonic Average Percentage | n / (Sum of (1/percentage)) | Scenarios with varying rates |
| Median Average Percentage | Middle value of the ordered set of percentages | Non-normal distributions |

In summary, calculating the average percentage is a vital task that can be performed using various methods, each with its own strengths and applications. By understanding the different methods and their formulas, individuals can choose the most suitable approach for their specific needs and make informed decisions.
What is the difference between simple and weighted average percentage?
+
The simple average percentage gives equal weight to all percentages, while the weighted average percentage assigns different weights to each percentage based on its importance or frequency.
When to use the geometric average percentage?
+
The geometric average percentage is used to calculate the average growth rate of a quantity over a period, making it suitable for finance and investment calculations.
What is the advantage of using the median average percentage?
+
The median average percentage is more robust to outliers and non-normal distributions, providing a better representation of the data in such scenarios.