Calculate P Value In Excel

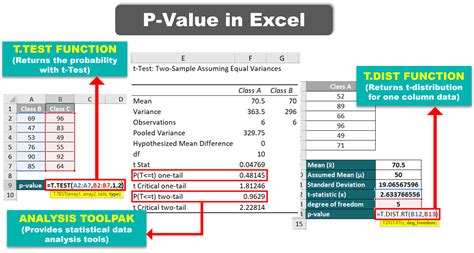
Introduction to Calculating P-Value in Excel

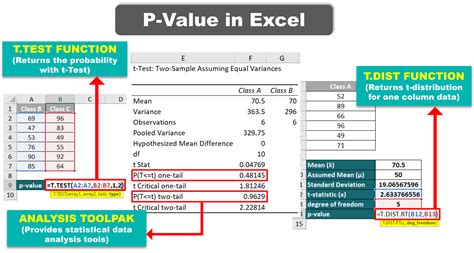
When conducting statistical tests, one of the key values that researchers and analysts look for is the P-value. The P-value, or probability value, is a measure that helps determine the significance of the results. In essence, it tells us whether the observed data would be highly unlikely under the null hypothesis, thereby suggesting that the null hypothesis should be rejected. Calculating the P-value can be complex, but fortunately, Microsoft Excel provides several functions and tools that make this process more manageable. In this article, we will explore how to calculate the P-value in Excel for various types of statistical tests.

Understanding P-Value

Before diving into the calculation, it’s essential to understand what the P-value represents. The P-value is the probability of observing results at least as extreme as those observed during the experiment or study, assuming that the null hypothesis is true. A small P-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, suggesting that the null hypothesis can be rejected, and the alternative hypothesis is supported.

Calculating P-Value in Excel

Excel offers several functions for calculating the P-value, depending on the type of statistical test being performed. Some common tests include the Z-test, T-test, and Chi-square test.

For a Z-Test

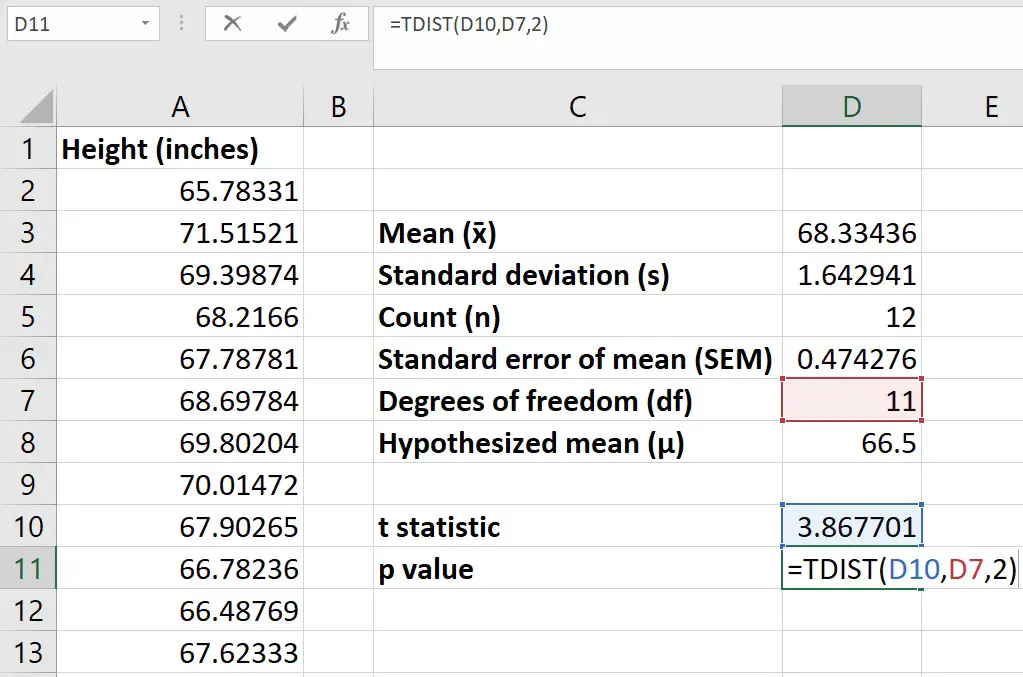
The Z-test is used when the population standard deviation is known. To calculate the P-value for a Z-test in Excel, you can use the ZTEST function or calculate it manually using the standard normal distribution (NORM.S.DIST or NORMSDIST function).

• Using ZTEST Function: The syntax for the ZTEST function is ZTEST(array, x, [sigma]), where array is the range of data, x is the value of the test statistic, and [sigma] is the population standard deviation. However, this function returns the P-value directly.

• Manual Calculation: If you prefer to calculate the Z-score first and then find the P-value, you can use the formula Z = (X - μ) / σ, where X is the sample mean, μ is the population mean, and σ is the population standard deviation. Then, use the NORM.S.DIST function to find the P-value. The syntax is NORM.S.DIST(z, cumulative), where z is the Z-score and cumulative is a logical value that indicates whether to return the cumulative distribution (TRUE) or the probability density (FALSE).

For a T-Test

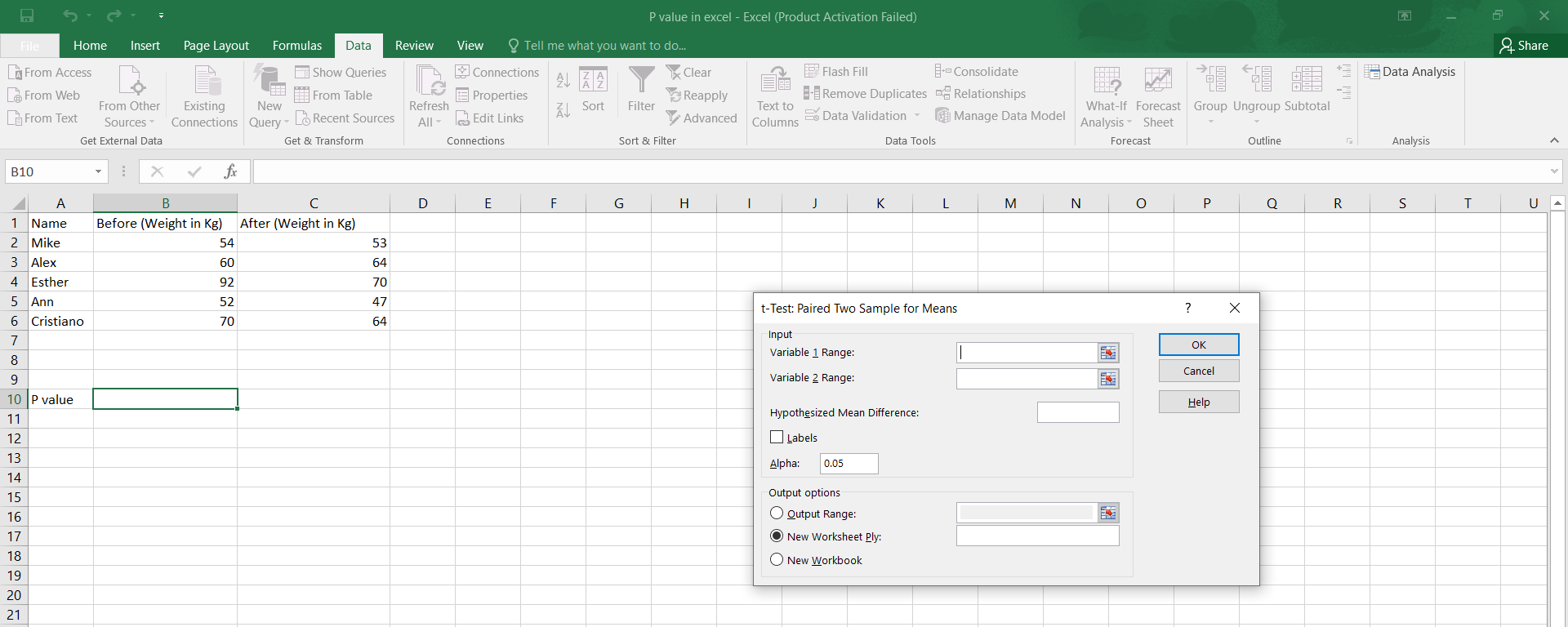
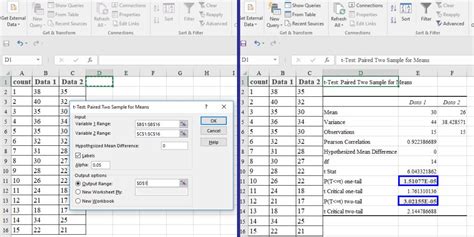
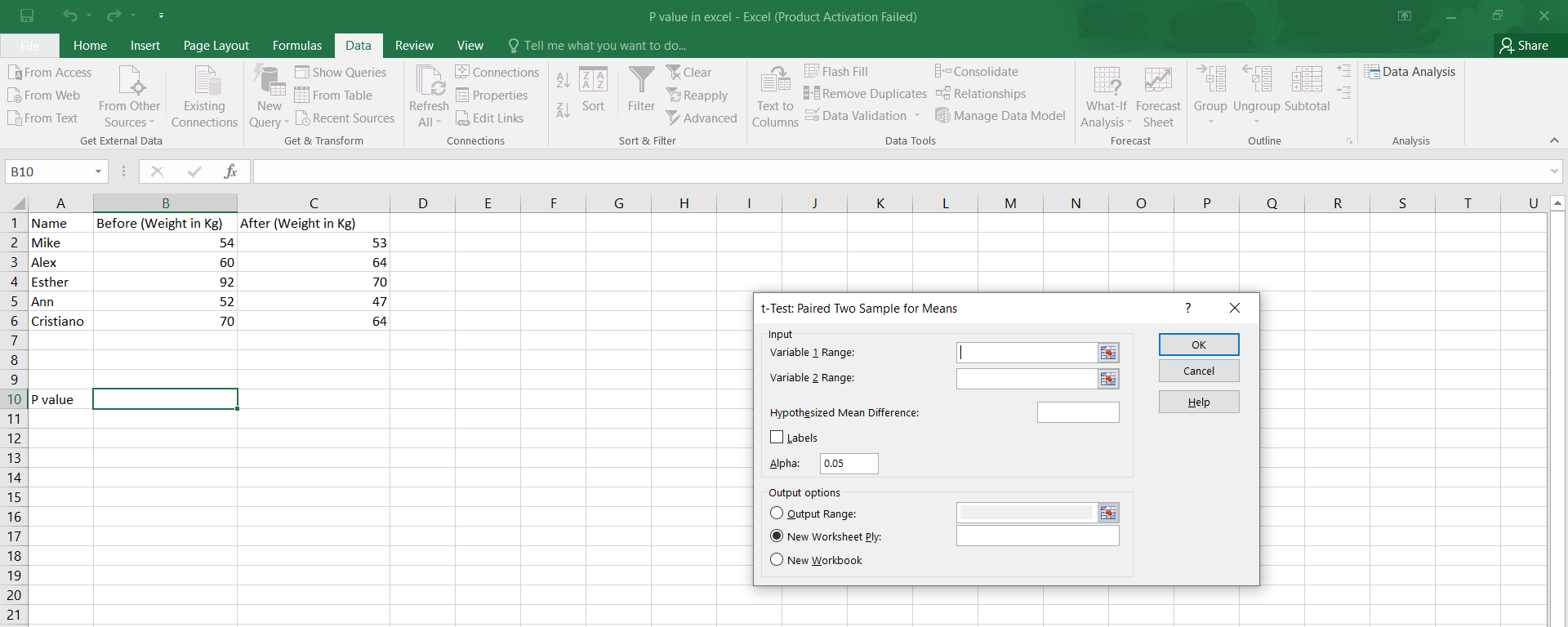
The T-test is used when the population standard deviation is unknown. Excel provides a TTEST function for calculating the P-value of a T-test. The syntax for the TTEST function varies depending on the type of T-test (one-sample, two-sample, or paired):

• One-Sample T-Test: TTEST(array, x, [tails], [type]), where array is the range of data, x is the hypothesized mean, [tails] specifies whether the test is one-tailed or two-tailed, and [type] is not used in this context.

• Two-Sample T-Test (assuming equal variances): TTEST(array1, array2, [tails], [type]), where array1 and array2 are the ranges of the two data sets, [tails] specifies the type of test, and [type] is set to 2 for a two-sample test assuming equal variances.

• Two-Sample T-Test (assuming unequal variances): Similar to the equal variances case, but [type] is set to 3.

For a Chi-Square Test

The Chi-square test is used for categorical data. Excel doesn’t have a built-in Chi-square test function like CHISQ.TEST, but you can calculate the Chi-square statistic manually and then use the CHISQ.DIST.RT function to find the P-value.

• Manual Calculation: Calculate the Chi-square statistic using the formula for your specific test, then use CHISQ.DIST.RT(x, deg_freedom), where x is the Chi-square value and deg_freedom is the degrees of freedom for the test.

Example Calculations

Let’s consider an example for each type of test mentioned above to illustrate how to calculate the P-value in Excel.

Example for Z-Test

Suppose we want to test if the average height of a population is 175 cm with a known standard deviation of 5 cm, given a sample mean of 178 cm from 100 observations.

1. Calculate the Z-score: Z = (178 - 175) / (5 / sqrt(100)) = 3 / 0.5 = 6
2. Use the NORM.S.DIST function: =NORM.S.DIST(6, TRUE) to get the cumulative probability, which gives us the P-value for a one-tailed test. For a two-tailed test, we multiply this value by 2.

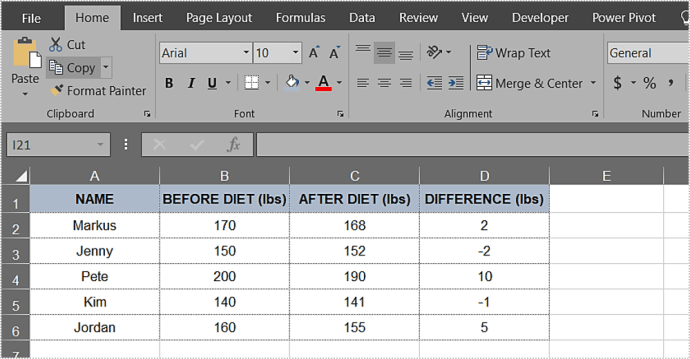
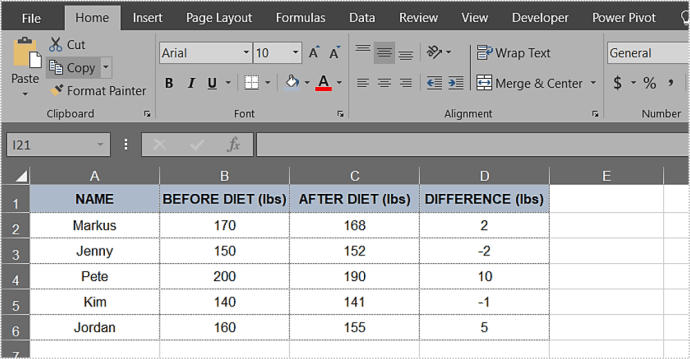
Example for T-Test

For a one-sample T-test, suppose we have a sample of exam scores with a mean of 85 and we want to test if this is significantly different from a population mean of 80, with a sample standard deviation of 10 and a sample size of 20.

1. Use the TTEST function: =TTEST(A1:A20, 80, 2, 1), assuming the data is in cells A1:A20.

Example for Chi-Square Test

Suppose we conducted a survey and want to test if there’s a significant association between two categorical variables. After calculating the Chi-square statistic manually, we use the CHISQ.DIST.RT function.

1. Calculate the Chi-square statistic manually based on observed and expected frequencies.
2. Use =CHISQ.DIST.RT(calculated_chi_square, degrees_of_freedom) to find the P-value.

💡 Note: Ensure that the degrees of freedom for the Chi-square test are calculated correctly based on the number of categories in your variables.

Interpreting P-Values

Once you have calculated the P-value, it’s crucial to interpret it correctly. A small P-value (typically < 0.05) indicates strong evidence against the null hypothesis, suggesting that the observed effects are statistically significant. A large P-value indicates weak evidence against the null hypothesis, suggesting that the observed effects might be due to chance.

Conclusion and Further Steps

Calculating the P-value in Excel is a straightforward process once you understand the appropriate functions and formulas to use. Whether you’re conducting a Z-test, T-test, or Chi-square test, Excel provides the tools you need to determine the statistical significance of your results. Remember to interpret your P-values in the context of your research question and to consider the limitations and assumptions of your statistical tests. By mastering the calculation and interpretation of P-values, you can make more informed decisions based on data analysis.